[240404] 클러스터링 분석 - ④ K-means 군집화

[파이썬으로 하는 클러스터링 분석 by 강민구 튜터]

1. K-means 군집화 (K-means Clustering)

1) 정의 

- Centroid라는 중심점과의 평균 거리를 활용해 K개 군집을 만드는 방법

- 대표적인 분리형 군집화 방법 중 하나 
└ 계층적 군집화와 달리, 전체 데이터의 구간을 나누어 클러스터를 만드는 방법

└ 모든 데이터 포인트는 하나의 클러스터에만 속할 수 있음

- Python Scikit-Learn에 구현된 K-means 알고리즘은 유클리디언 거리 기반

출처 -  https://towardsdatascience.com/the-5-clustering-algorithms-data-scientists-need-to-know-a36d136ef68

 

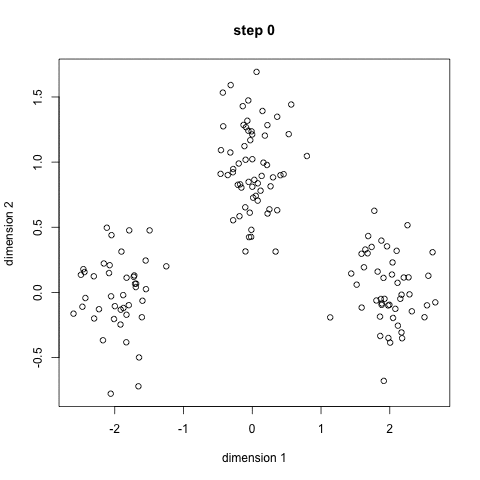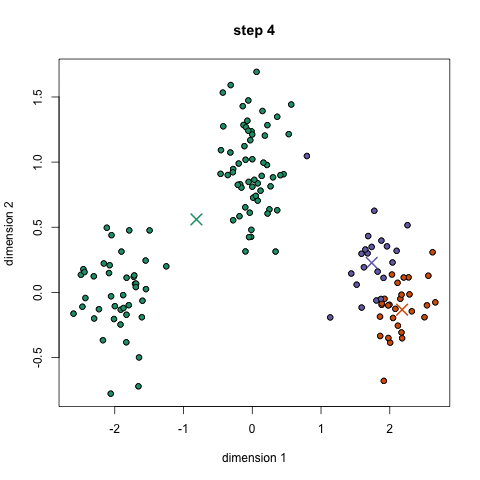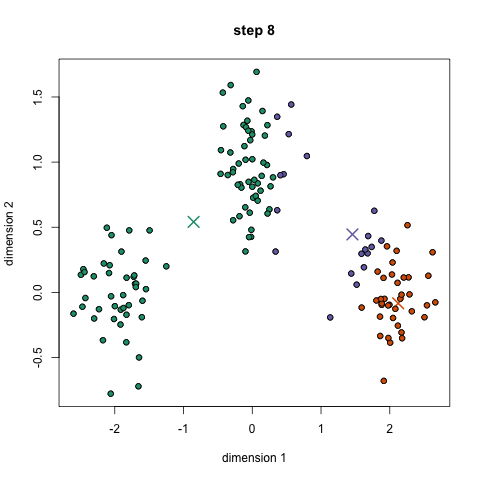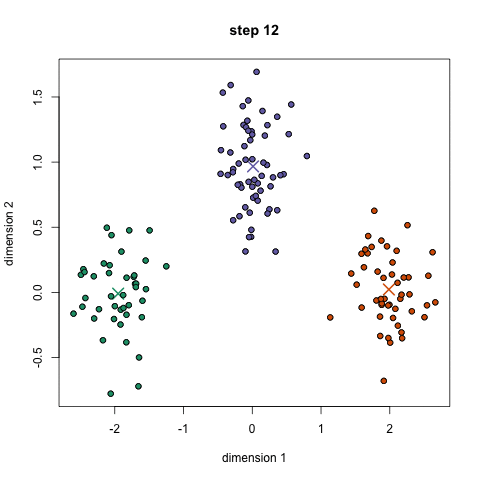
- K-means 알고리즘의 목적 

 ① Centroid의 최적화: 최적의 Centroid 위치 선정 

 ② Membership 최적화: 각각의 데이터 포인트를 K개의 클러스터 중 최적의 한 곳에 할당

- 군집개수인 K는 사용자가 직접 지정해야 하는 하이퍼 파라미터 값에 해당 

- 초기 임의로 정해지는 Centroid의 위치가 최종 클러스터 결과에 중요한 역할
 └ Centroid는 실제 데이터 포인트일 수도 있고, 임의의 포인트일 수도 있음
 
2) K-means clustering의 장점과 한계 

(1) 장점 
 ① 빠른 속도 
  - 계산에 드는 비용(시간과 메모리)이 적은 편
  - 많은 양의 데이터나 고차원 데이터도 빠르게 클러스터링 가능 
 ② 단순한 알고리즘 
  - 알고리즘 자체도 간단한 편이라 빠르게 구현해서 클러스터링 결과를 볼 수 있음
 ③ 빠르고 단순하게 클러스터링 가능 
  - 실무에서 굉장히 큰 장점 

(2) 한계
 ① 클러스터 개수 지정 필요 
  - K값에 따라 클러스터링 결과가 완전 달라질 수 있음 
  - 데이터 특성을 잘 모를 경우 적절한 K값 지정이 어려움 
 ② 다양한 데이터 분포 및 특성 반영의 한계  (유클리디안 거리 기반 동작의 한계
  - 서로 다른 크기 또는 밀도의 군집을 찾아내기 어려움 
  - 데이터가 구(Sphere) 형태가 아닌 다른 특성이 있는 형태일 경우 클러스터링 성능이 떨어짐

  - 유클리디안 거리 기반으로 동작하기 때문
 ③ Outlier에 취약
  - 유클리디안 거리 기반으로 동작하기 때문

출처 - https://towardsdatascience.com/k-means-clustering-algorithm-applications-evaluation-methods-and-drawbacks-aa03e644b48a

3) K-Means Clustering 진행 과정 

출처 - https://github.com/pilsung-kang/Business-Analytics-ITS504-/blob/master/07 Clustering/07-2_K-Means Clustering.pdf

 

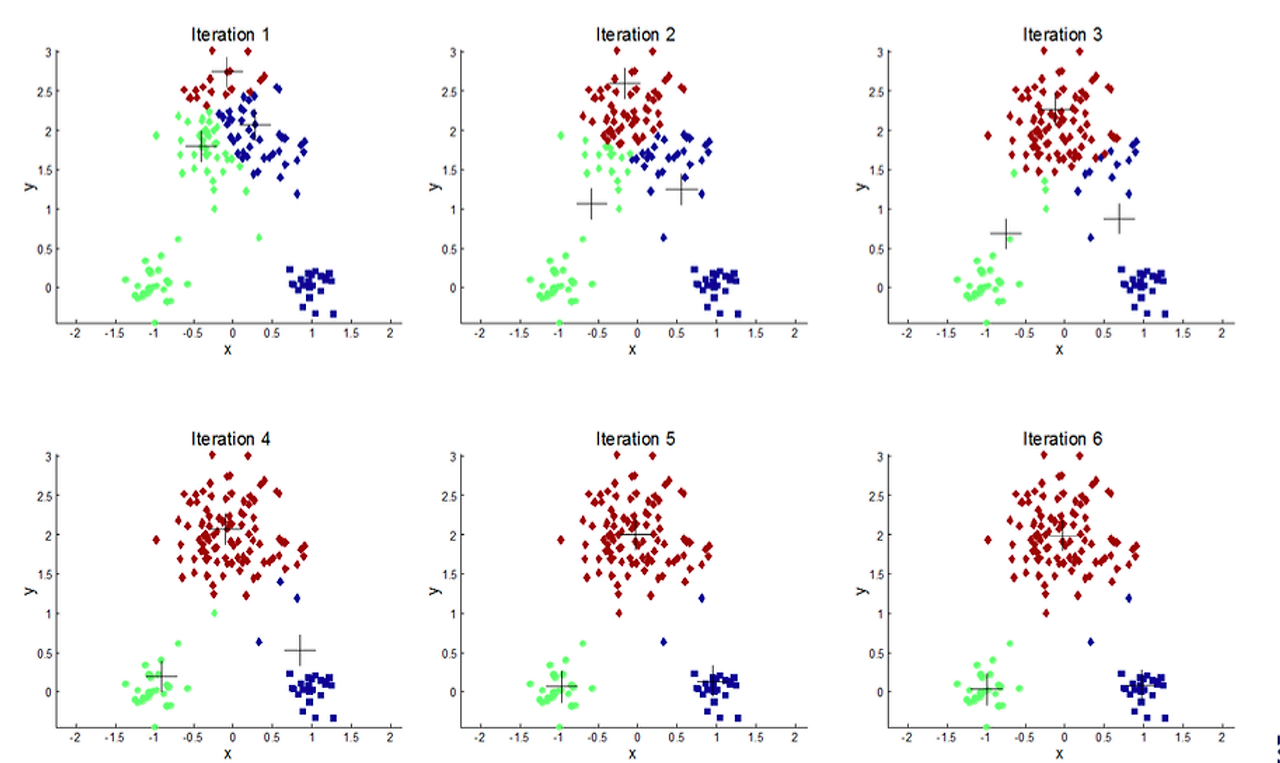
 ① 사용자가 지정한 K에 따라 K개의 Centroid를 지정
 ② 수렴 조건에 만족할 때까지 아래 작업을 반복
  └ 각 데이터 포인트들과 Centroid 사이 거리를 계산해 가장 가까운 Centroid에 따라 라벨(Membership) 부여
  └ 구성된 K개의 클러스터에 대해 각각의 Centroid를 다시 계산

  └ 새롭게 계산된 Centroid 값이 직전 Centroid 값과 동일(수렴 조건 만족)한 경우에 반복을 멈춤 

  (참고) 수렴이 안 되는 경우를 방지하고자 최대 반복 횟수(max iteration)를 지정하기도 하나, 웬만하면 빠르게 수렴됨

 

2. 클러스터링 결과 평가

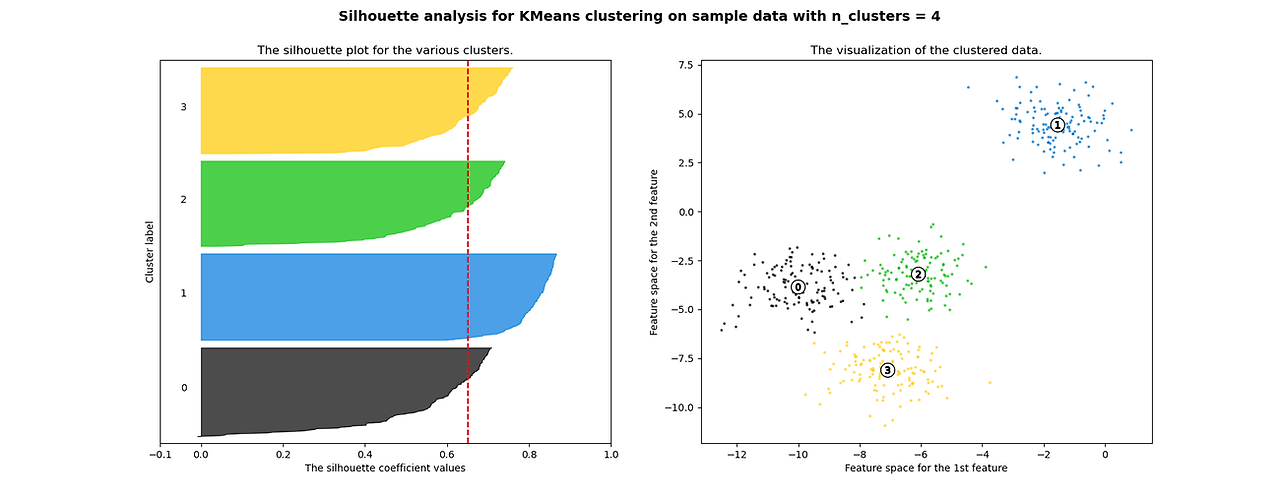
1) 실루엣 계수 (Silhouette coefficient)
- 클러스터링 결과의 타당성을 평가하는 데 자주 사용되는 지표

- 클러스터 내 거리(compactness)는 가깝고, 클러스터 간 거리(separation)는 멀수록 높은 점수  

- 클러스터 개수로 설정한 K값이 적절한지를 알아보는 데 도움을 줌 

출처 -  https://www.researchgate.net/figure/Silhouette-coefficient-example_fig2_272017073

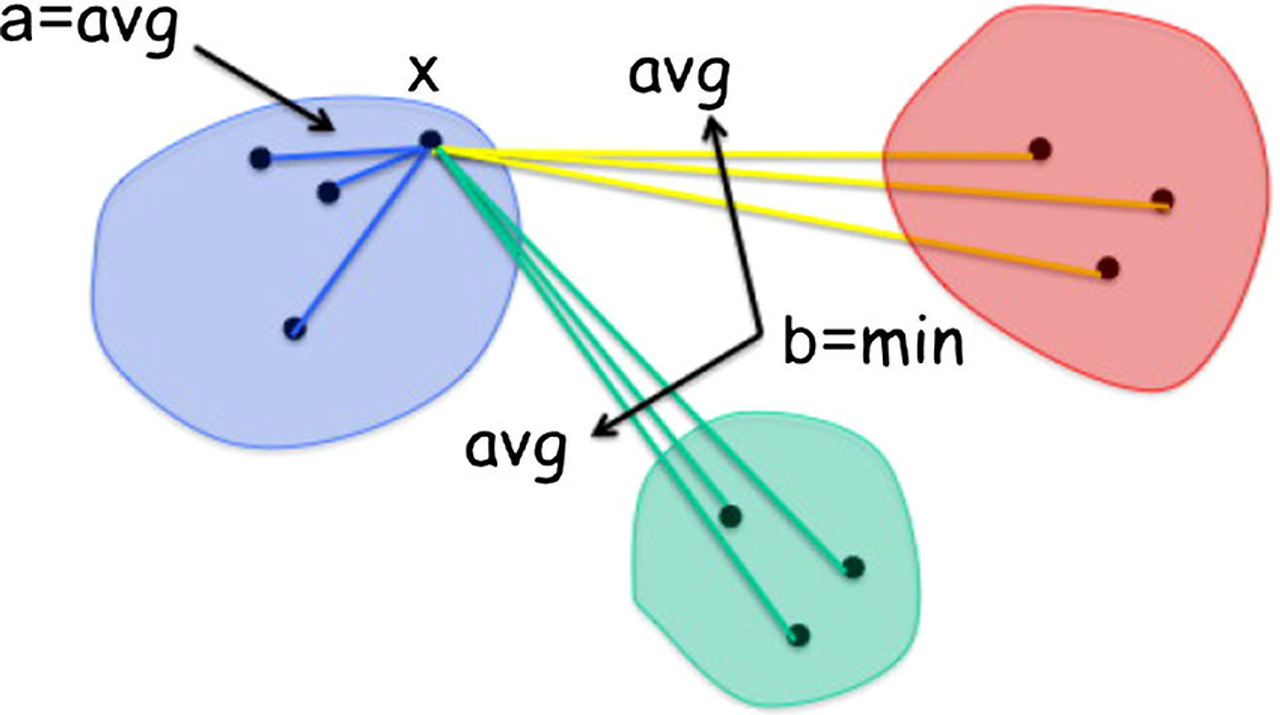
2) 실루엣 계수 계산 방법

출처 - https://dashee87.github.io/data science/general/Clustering-with-Scikit-with-GIFs/

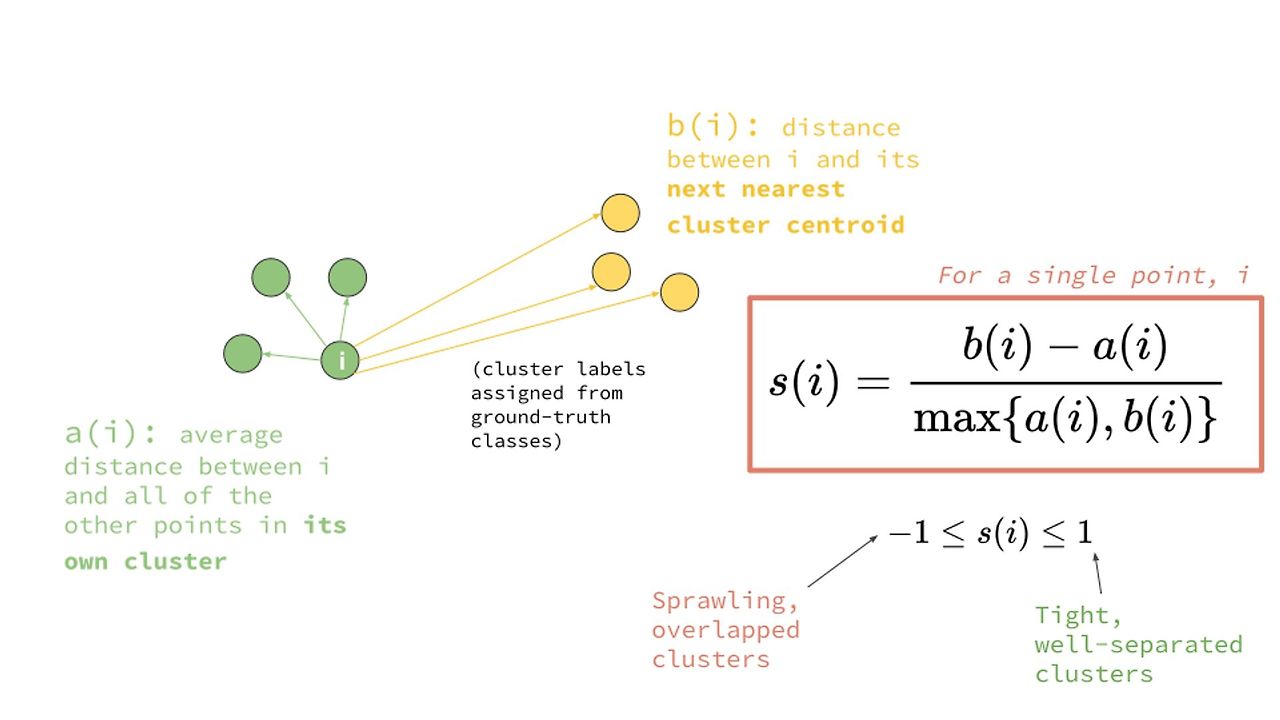
① 어떤 데이터 포인트 i 에 대해 아래 두 값을 계산
  - a(i) : i와 같은 군집에 속한 데이터 포인트들과 i 사이의 거리 평균 
  - b(i) : i가 속한 군집과 거리가 가장 가까운 군집에 속한 데이터 포인트들과 i 사이의 거리 평균
② 데이터 포인트 i 에 대한 실루엣 계수 s(i)는 위 그림 속 식으로 계산

  - (군집간 평균 거리 - 군집내 평균 거리) / (군집간, 군집내 평균 거리 중 최대값) 

  - 최솟값은 -1 : b(i) = 0 인 경우이나 실제로 거의 나타나기 힘든 값
  - 최댓값은 1 : a(i) = 0 인 경우로 한 군집의 모든 데이터가 같은 지점에 있다는 뜻
③ 각각의 데이터 포인트에 대한 실루엣 계수를 평균낸 결과가 해당 데이터셋의 실루엣 계수

출처 -  https://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_silhouette_analysis.html

3. K-means 응용

 1) K-means ++

  ① K-means 초기 Centroid의 중요성

출처 -  https://www.geeksforgeeks.org/ml-k-means-algorithm/

 

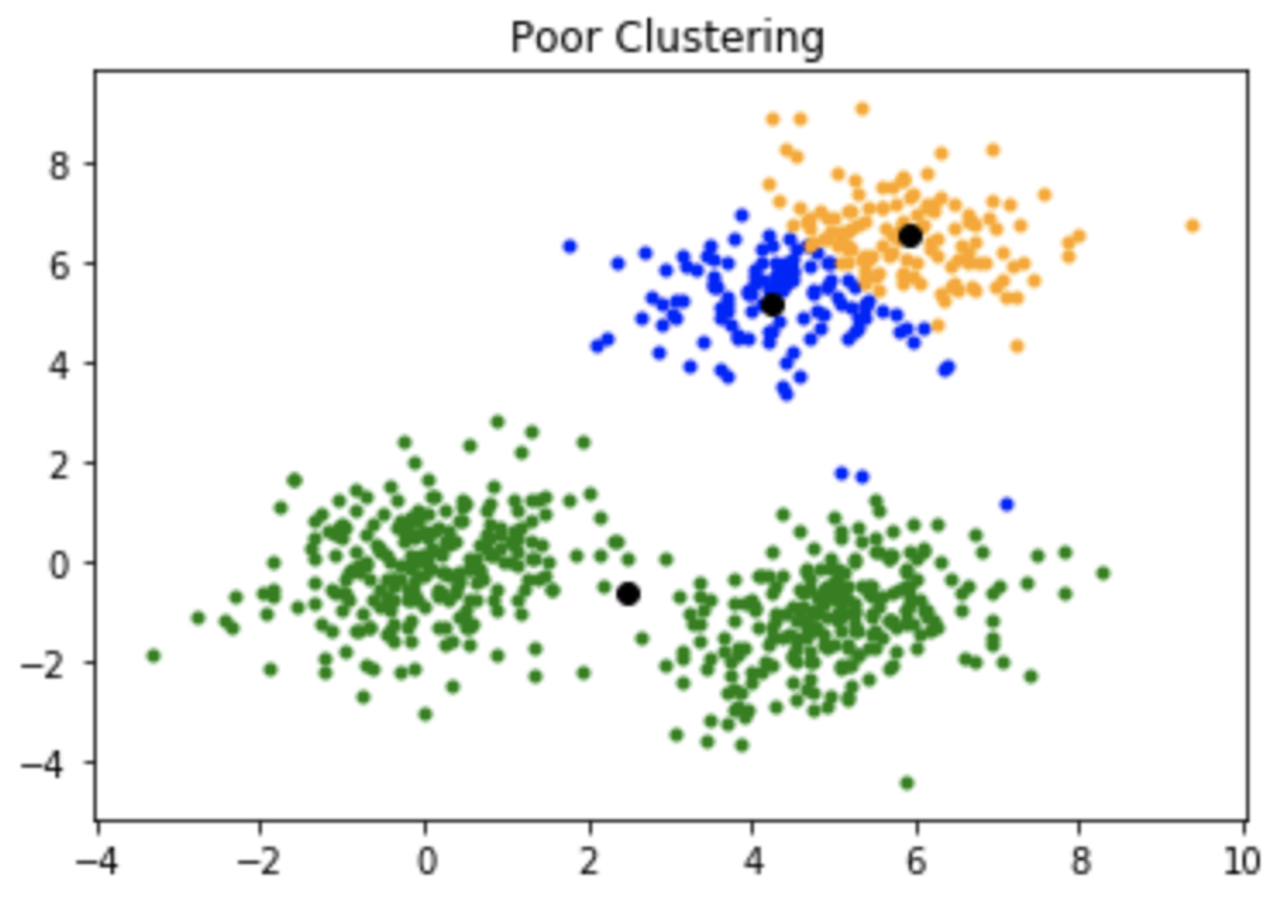
- 문제: 초기 Centroid가 데이터 분포를 무시한 채 할당되면 좋지 않은 클러스터링 결과가 나올 수 있음 

 └ K-means 알고리즘의 수렴 조건은 Centroid가 변하지 않을 때이므로 초기 Centroid에 영향을 많이 받는 것 

- 해결책 1: 최대한 여러 번 K-means를 실행해보는 것

 └ Centroid가 적당한 곳에 위치하면 수렴되는 Centroid 지점이 비슷해짐 

 └ 같은 데이터에 대해 알고리즘을 여러 번 실행해 가장 자주 나타나는 클러스터링 결과 선택

- 해결책 2: Centroid를 적절하게 설정하기 위한 알고리즘을 활용하거나 사용자가 직접 Centroid 위치 지정

② K-means ++를 활용한 초기 Centroid 설정

출처 -  https://www.geeksforgeeks.org/ml-k-means-algorithm/

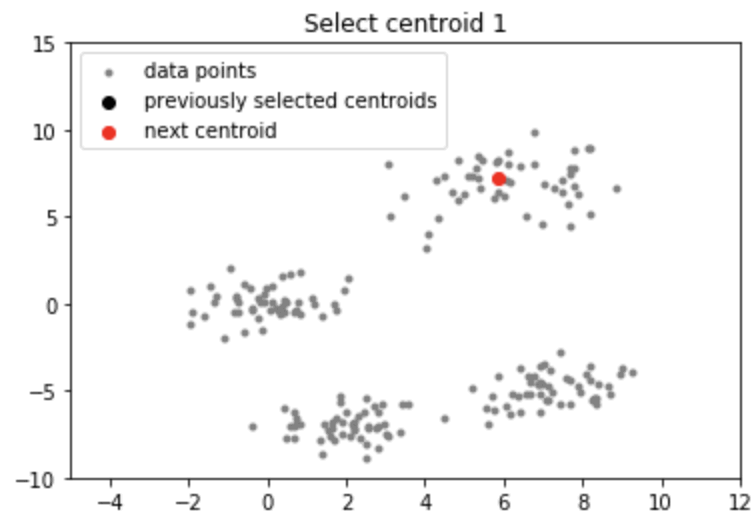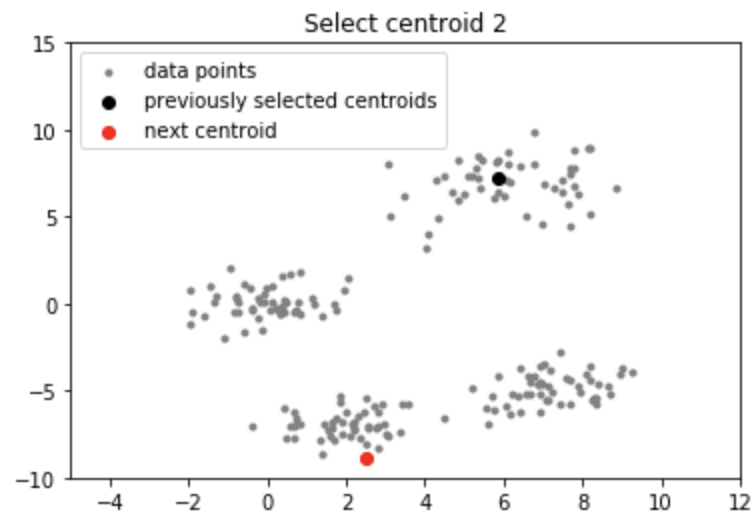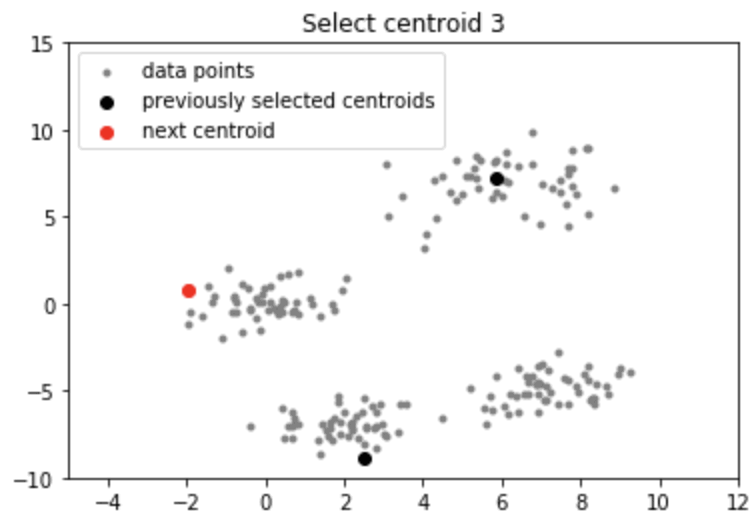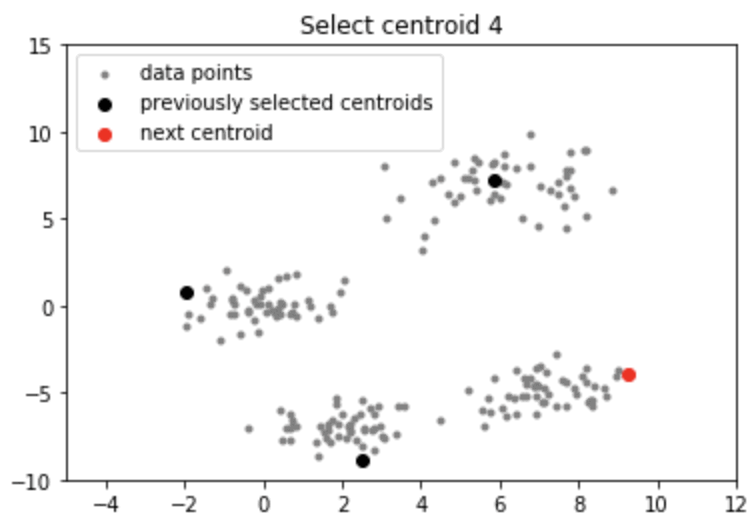
- K-means++는 초기 Centroid를 최대한 멀리 퍼뜨리기 위한 방법 중 하나
- K-means++ 작동 로직

  (1) 데이터 포인트 중 랜덤하게 하나의 값을 선택
  (2) 모든 데이터 포인트에 대해서 가장 가까운 Centroid와의 거리를 계산
  (3) (2)에서 계산한 거리가 가장 먼 점일 수록 다음 Centroid로 선택될 확률 증가 

  (4) K개의 Centroid가 선택될 때까지 이를 반복

 

2) Cosine 거리를 활용한 K-means

- 다차원 데이터에서 성능을 높이기 위한 방법

└ K-means는 유클리디언 거리를 활용하므로 고차원 데이터일 수록 성능에 한계가 있음 

└ 이유1: 차원이 늘어날 수록 거리가 커지는 경향

└ 이유2: 벡터 크기만 고려하고 방향성을 고려하지 않기 때문에 유클리디언 거리로 설명엔 한계

 - Cosine 거리를 활용해 K-means 클러스터링 시 고차원 데이터(텍스트 분석 등)에서 성능 보다 우수 

- 자세한 설명은 Spherical k-means for document clustering 블로그 참조 

└ 관련 패키지까지 포함돼 있음!

 

(부록) 참고자료
- [고려대학교 강필성 교수님 강의: Clustering - Overview]
- [고려대학교 강필성 교수님 강의: Clustering - K-means Clustering]
- [The Silhouette Loss Function: Metric Learning with a Cluster Validity Index]
- [K-means++ Algorithm]