[파이썬으로 하는 클러스터링 분석 by 강민구 튜터]
1. 클러스터 개념과 거리
1) 클러스터링 정의
- 사전적으로 클러스터링(Clustering)은 서로 가까이 있는 비슷한 것들의 그룹(군집)을 이루는 작업

- 데이터 분석 기법에서 클러스터링은 분석 대상이 되는 데이터의 그룹을 만드는 방법론

- 그룹은 마구잡이로 만드는 것이 아니라, 특정 기준인 '데이터 사이의 거리'를 바탕으로 생성
└ intra-cluster(군집 내 거리): 군집 내 데이터 간 거리가 가까울수록 좋음
└ inter-cluster(군집 간 거리): 각각의 군집 사이의 거리는 멀수록 좋음
- 데이터 특성이나 분석가 주관에 따라 같은 데이터라도 둘 사이 거리를 다르게 판단할 수 있음
2) 클러스터링 활용 예시
① Summarization

- 데이터 그룹을 묶어 각 군집 특성을 파악한다면, 모든 데이터를 확인하지 않아도 전체 데이터 특성 확인 가능
- 데이터 시각화와 연관된 경우가 많음
- (예시) 1년간의 뉴스 데이터를 클러스터링하여 그 해의 주요 뉴스 토픽 찾기 등
② Understanding

- 클러스터링을 통해 데이터의 분포 및 특성을 확인 가능
- 라벨링(labeling)이 되어있지 않은 데이터를 살펴볼 때 효과적
- (예시) Spotify에서 1년간 재생된 음악들의 특성 분석, 카드 사용 패턴에 따른 고객 세그먼트 클러스터링 등
③ Strategy Planning

- 클러스터링이 활발히 활용되는 분야로 분석가의 분석 능력이 요구됨
- 클러스터링 결과를 통해 데이터 분석을 통한 Action Item 도출 가능
- (예시)
└ 이상치 탐지(Anomaly Detection): 클러스터링 이후 군집의 중심에서 크게 떨어져 있는 데이터를 조사
└ 유저 필터링: 서비스 사용을 활발하게 하는 유저가 포함된 군집을 탐색하여 해당 군집 대상으로 인터뷰를 진행
3) 다양한 종류의 거리(Distance)
① 유클리디안 거리 (Euclidean distance)

- 두 지점 사이 최단 거리를 계산하는 방식
- 일반적으로 가장 익숙한 거리 계산식으로 피타고라스 거리, 직선 거리로도 불림
- 데이터 차원이 크지 않은 경우 사용하며, 차원이 클수록 값이 커져 효과가 떨어짐
- 일반 수식
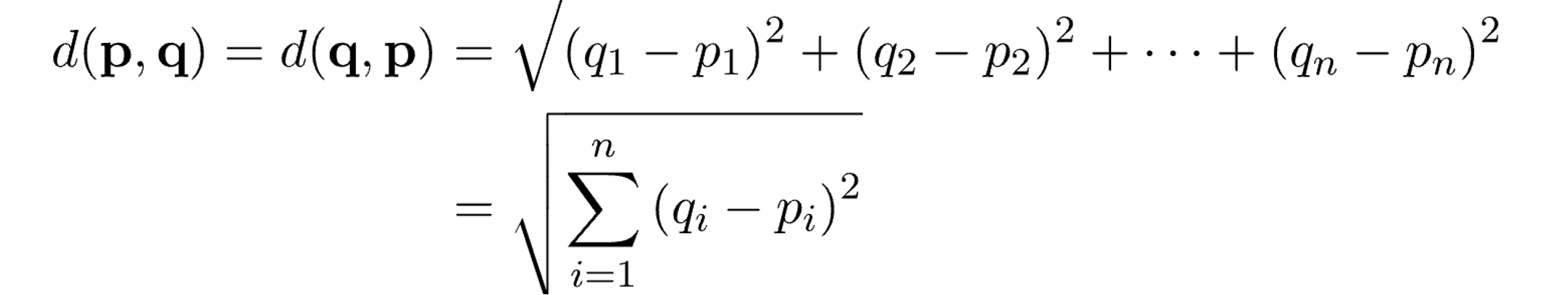
▶ 실습 코드
① 라이브러리 & 데이터 불러오기 (이하 동일)
import numpy as np
import pandas as pd
from sklearn import datasets
data_iris = datasets.load_iris()
iris1 = data_iris['data'][0]
iris2 = data_iris['data'][1]
iris3 = data_iris['data'][-1]
② 유클리디안 거리
# 유클리디안 거리 Euclidean distance 계산 함수
# 계산식: (차원x1 - 차원x2) 제곱의 총합/시그마 -> 제곱근(루트) 한 값
def euclidean_dist(x1, x2):
'''
input: (array of float, array of float)
output: float
'''
dist = 0
for a, b in zip(x1, x2):
dist += (a - b)**2
return dist ** 0.5
# iris1, iris2 수기 계산식:(((5.1-4.9)**2)+((3.5-3.0)**2)) **0.5 = 0.5385164807134502
print(euclidean_dist(iris1, iris2)) # 0.5385164807134502
print(euclidean_dist(iris1, iris3)) # 4.1400483088968905
print(euclidean_dist(iris2, iris3)) # 4.153311931459037
- sklearn 활용
# 유클리디안 거리 Euclidean distance Scikit-Learn으로 계산하기
# https://scikit-learn.org/stable/modules/generated/sklearn.metrics.pairwise.euclidean_distances.html
from sklearn.metrics.pairwise import euclidean_distances
# 왜 return 값에 []를 넣어줘야 하는가?
# sklearn은 모든 경우 2D array가 들어올 것을 기대(data, features)
# 1D array나 list로 들어가면, 하나의 feature에 여러 개 data가 있는지, 여러 features에 data가 하나씩 있는지 알 수 없음
# 2D array는 list of list를 통해 생성 가능 [[x1], [x2]]
def euclidean_dist_sklearn(x1, x2):
#return euclidean_distances([x1], [x2]) #2차원 배열 만들기 위해 [] 추가 #결과값 [[0.53851648]] 이런 식으로 도출됨
return euclidean_distances([x1], [x2])[0][0] #[0][0] 넣어서 값만 나오도록 정리
print(euclidean_dist_sklearn(iris1, iris2)) # 0.5385164807134628
print(euclidean_dist_sklearn(iris1, iris3)) # 4.140048308896891
print(euclidean_dist_sklearn(iris2, iris3)) # 4.153311931459037
② 맨해튼 거리(Manhattan distance)
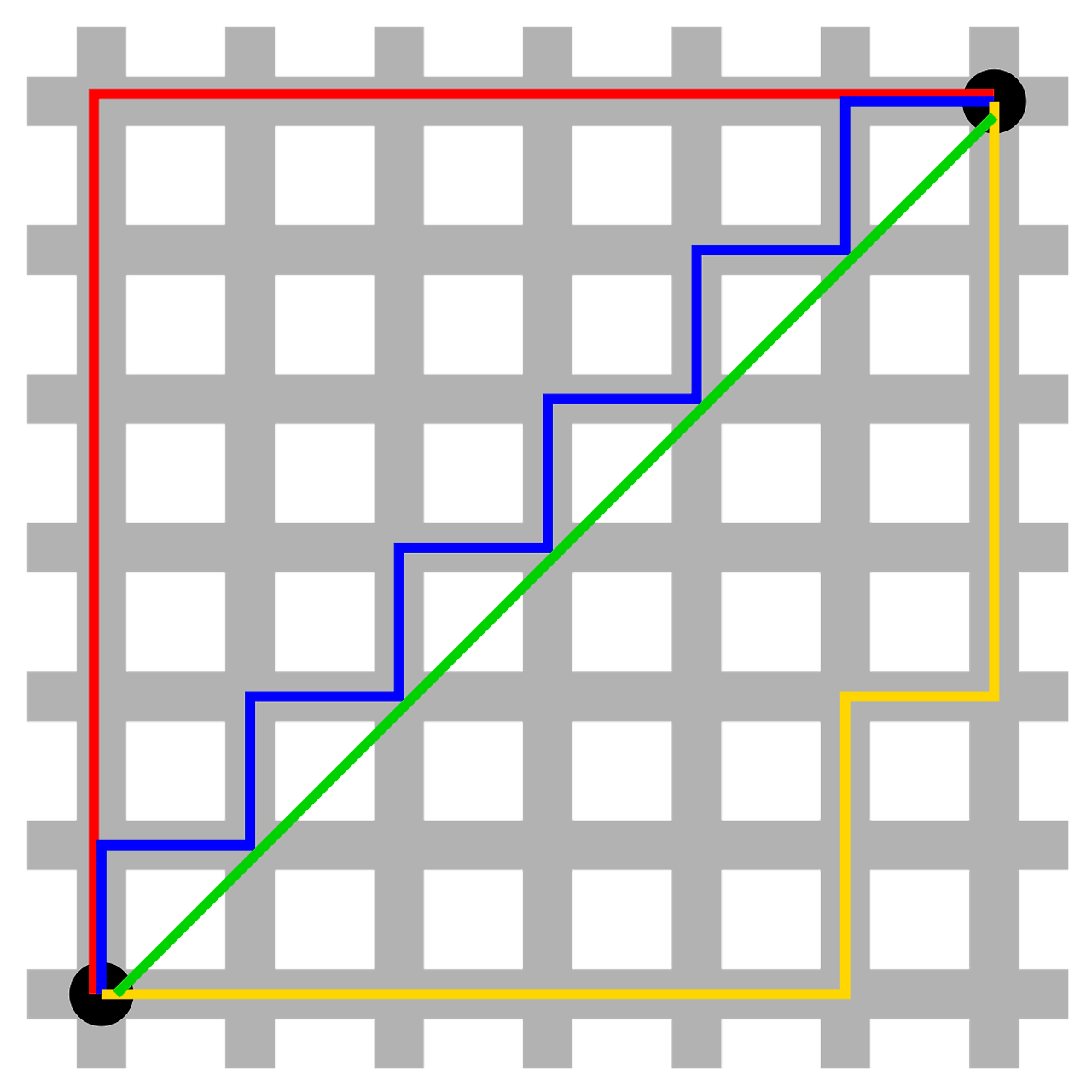
- 두 지점에 대한 각 차원 상 거리 차이의 합
- 2차원에서는 '맨해튼 거리 = X축 사이의 차이 + Y축 사이의 차이'
└ 바둑판 형태로 잘 정렬된 맨해튼에서 두 지점 사이를 이동할 때 걷는 거리 = 맨해튼 거리!
- 두 지점 사이 최적의 경로 계산을 하는 경우 사용 (ex. 내비게이션 등)
- 일반 수식
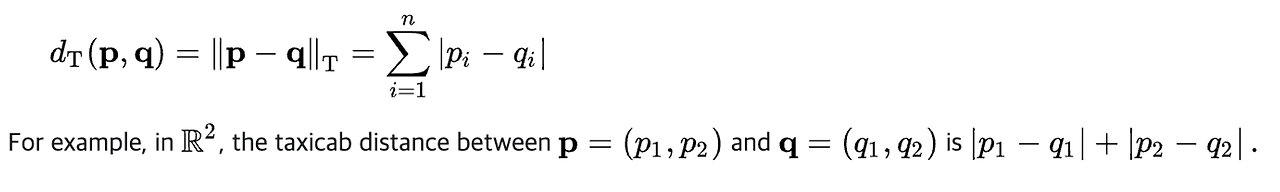
(참고) 📐 민코우스키 거리(Minkowski distnace)
- 맨해튼 거리, 유클리디언 거리의 계산식을 일반화한 거리 개념
└ p = 1인 경우 → 맨해튼 거리
└ p = 2인 경우 → 유클리디언 거리
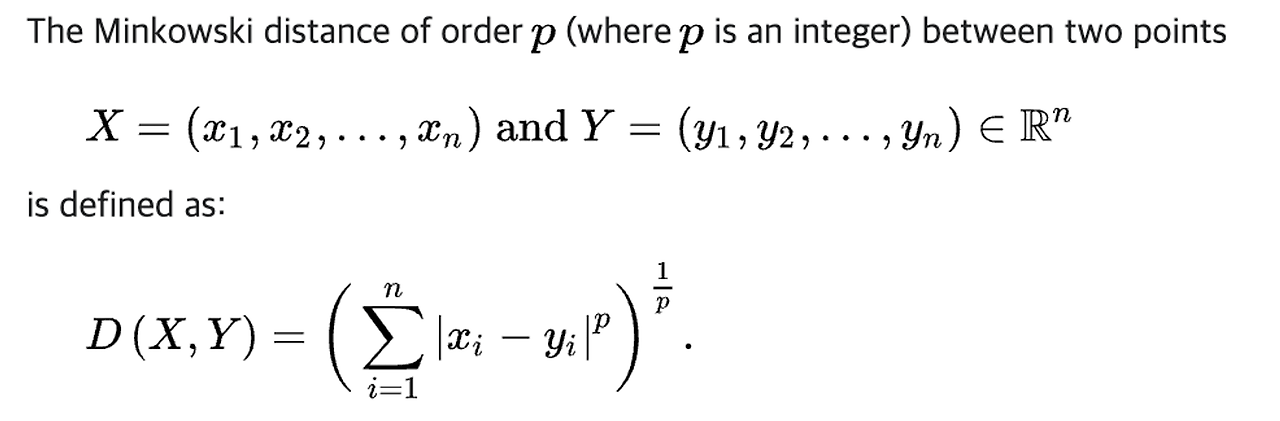
▶ 실습 코드
② 맨하튼 거리
# manhattan distance 계산 함수 1
# 계산식: 차원1(x1) - 차원(x-2)의 절대값 총합
# zip 함수 이용
def manhattan_dist(x1, x2):
'''
input: (array of float, array of float)
output: float
'''
dist = 0
for a, b in zip(x1, x2):
dist += abs(a-b)
return dist
# manhattan distance 계산 함수 2
# numpy 이용하면 더 간단: numpy는 각 원소별로 계산이 됨
def manhattan_dist_np(x1, x2):
'''
input: (array of float, array of float)
output: float
'''
dist = sum( abs(x1 - x2) )
return dist
# 결과값은 동일
print(manhattan_dist_np(iris1, iris2)) # 0.6999999999999993
print(manhattan_dist_np(iris1, iris3)) # 6.6
print(manhattan_dist_np(iris2, iris3)) # 6.299999999999999
- sklearn 활용
# Scikit-Learn을 활용한 manhattan 거리 계산
# https://scikit-learn.org/stable/modules/generated/sklearn.metrics.pairwise.manhattan_distances.html
from sklearn.metrics.pairwise import manhattan_distances
def manhattan_dist_sklearn(x1, x2):
return manhattan_distances([x1], [x2])[0][0]
print(manhattan_dist_sklearn(iris1, iris2)) # 0.6999999999999993
print(manhattan_dist_sklearn(iris1, iris3)) # 6.6
print(manhattan_dist_sklearn(iris2, iris3)) # 6.299999999999999
③ 코사인 거리(Cosine distance)
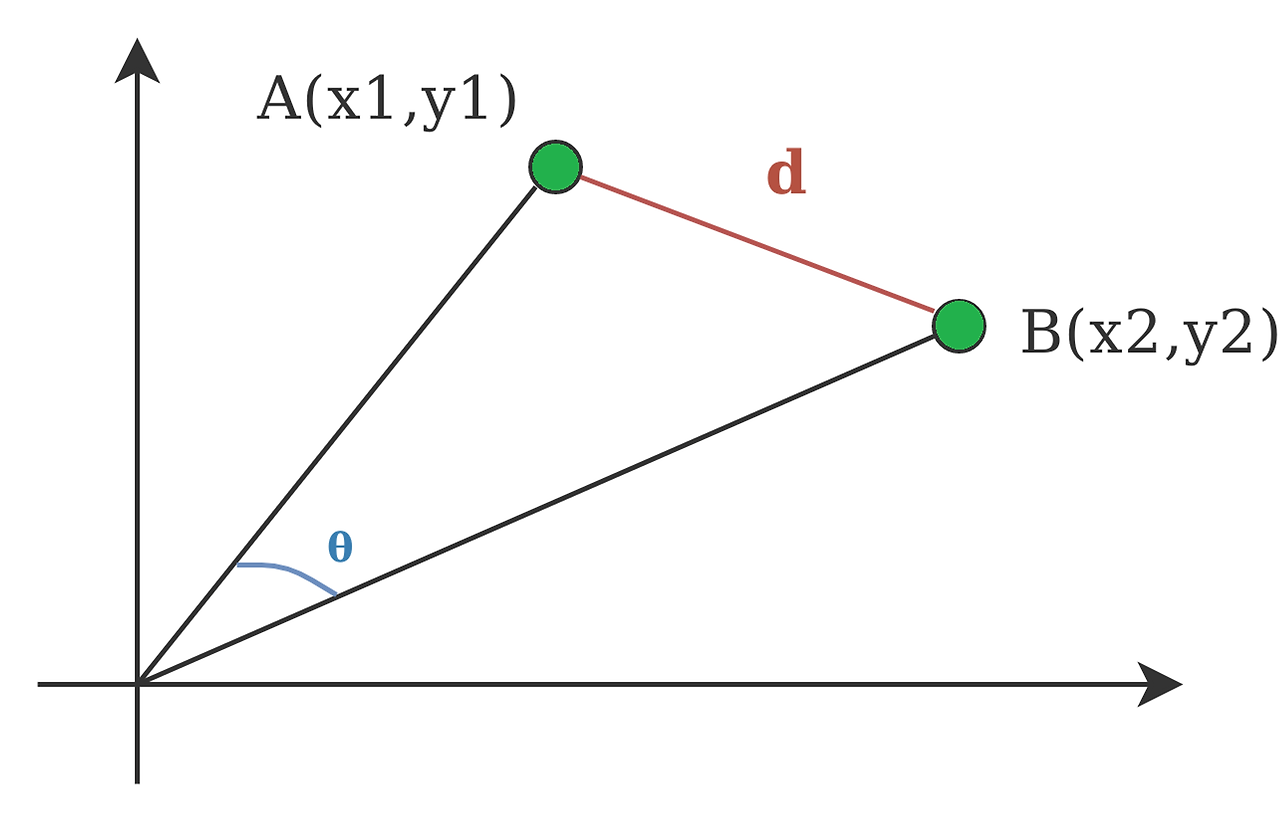
- 두 데이터 값의 방향성 차이를 측정한 거리
- 코사인 거리 = 1 - 코사인 유사도
└ 코사인 유사도를 측정한 뒤에 1을 빼면 거리로 변환됨
└ 코사인 유사도와 거리는 비슷한 개념이지만 방향이 반대이기 때문(ex. 두 데이터가 유사도가 크다 = 거리가 가깝다)
- 값 자체의 차이보다 방향성의 차이가 중요하거나 데이터 차원이 너무 큰 경우 사용
└ 유클리디안 거리보다 차원의 영향을 덜 받는 편
└ (예시) 주로 듣는 음악 ‘장르’에 따른 유저 간 거리(방향성), 텍스트 클러스터링(큰 차원)
- 일반 수식
└ 코사인 유사도(Cosine similarity)란?
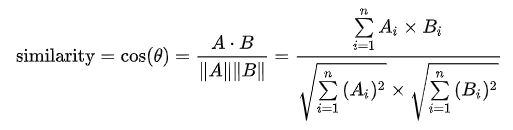
: 내적 공간의 두 벡터 간 각도의 코사인 값을 이용해 측정된 벡터 간 유사한 정도를 의미
: 각 벡터를 정규화한 후 스칼라 곱을 한 결과값은 두 벡터의 코사인 값과 일치
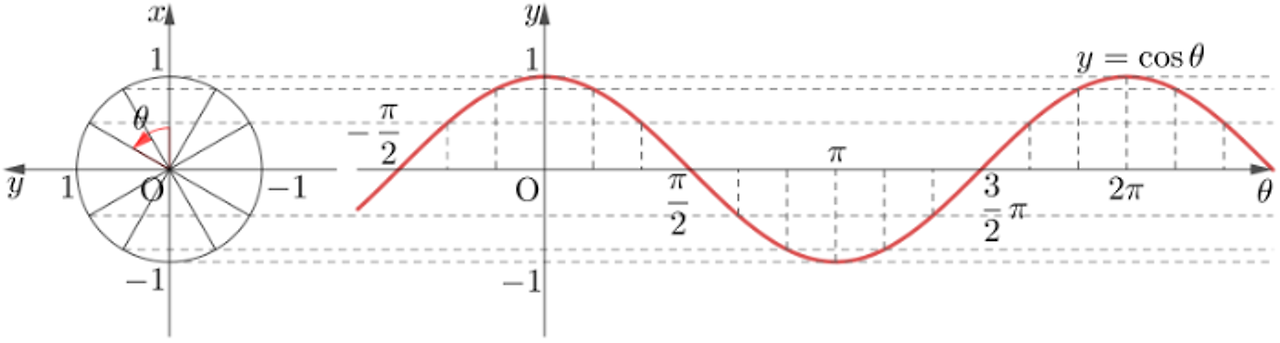
- 두 데이터 사이의 cosine 값을 계산하여 유사도 측정 가능
· θ = 0° 는 두 값의 방향이 동일하므로 cosine_similarity = 1
· θ = 90° 는 두 값의 방향이 직교하므로 cosine_similarity = 0
· θ = 180° 는 두 값의 방향이 반대이므로 cosine_similarity = -1
✍️ 용어 설명
- 벡터(vector): 크기와 방향을 갖는 개념
- 스칼라(scalar): 방향을 갖지 않고 크기만 갖는 개념
- 내적: 벡터를 수처럼 곱하는 개념으로 방향이 일치하는 만큼 두 벡터의 크기를 곱해 결과값으로 스칼라를 얻.
└ 스칼라곱(scalar product) 또는 점곱(dot product)이라고도 불림
▶ 실습 코드
③ 코사인 거리
# 데이터
dataset_music_dict = {"rock": [26, 60, 0, 2, 5],
"hiphop": [60, 60, 6, 19, 11],
"pop": [70, 60, 17, 210, 14],
"jazz": [35, 60, 1, 5, 7],
"ballad": [60, 60, 210, 8, 12]}
df_music = pd.DataFrame(dataset_music_dict)
df_music
# 참고
# 유클리디안 거리는 0과 1의 거리가 0과 4보다 가까우므로, 0과 1의 유사성이 높다는 결론
print(euclidean_dist_sklearn(df_music.iloc[0], df_music.iloc[1])) # 43.37049688440288
print(euclidean_dist_sklearn(df_music.iloc[0], df_music.iloc[4])) # 95.21554494934112
# cosine distance 계산 함수 1
# 계산식: 코사인 거리 = 1 - 코사인 유사도
# 코사인 유사도 = (차원1 * 차원2)의 총합 / 차원1 제곱 총합의 제곱근 * 차원2 제곱 총합의 제곱근
def cosine_dist(x1, x2):
'''
input: (array of float, array of float)
output: float
'''
co = 0
si = 0
sine = 0
for a, b in zip(x1, x2):
co += a * b
si += a**2
sine += b**2
cosine = co / ((si**0.5) * (sine**0.5))
dist = 1 - cosine
return dist
# cosine distance 계산 함수 2
# 힌트: list comprehension 활용해서 분모 생성
def cosine_dist(x1, x2):
'''
input: (array of float, array of float)
output: float
'''
co_x1 = sum(a**2 for a in x1) ** 0.5
co_x2 = sum(b**2 for b in x2) ** 0.5
dist = 0
for c, d in zip(x1, x2):
dist += c * d
dist = dist / (co_x1 * co_x2)
return 1 - dist
print(cosine_dist(df_music.loc[0], df_music.loc[1])) # 0.051343052747109375
print(cosine_dist(df_music.loc[0], df_music.loc[4])) # 0.0006884388180635748
- sklearn 활용
# Scikit-Learn을 활용한 cosine 거리 계산
# https://scikit-learn.org/stable/modules/generated/sklearn.metrics.pairwise.cosine_distances.html
from sklearn.metrics.pairwise import cosine_distances
def cosine_dist_sklearn(x1, x2):
return cosine_distances([x1], [x2])[0][0]
print(cosine_dist_sklearn(df_music.loc[0], df_music.loc[1])) # 0.051343052747109263
print(cosine_dist_sklearn(df_music.loc[0], df_music.loc[4])) # 0.0006884388180635748
④ 자카드 유사도(Jaccard similarity)
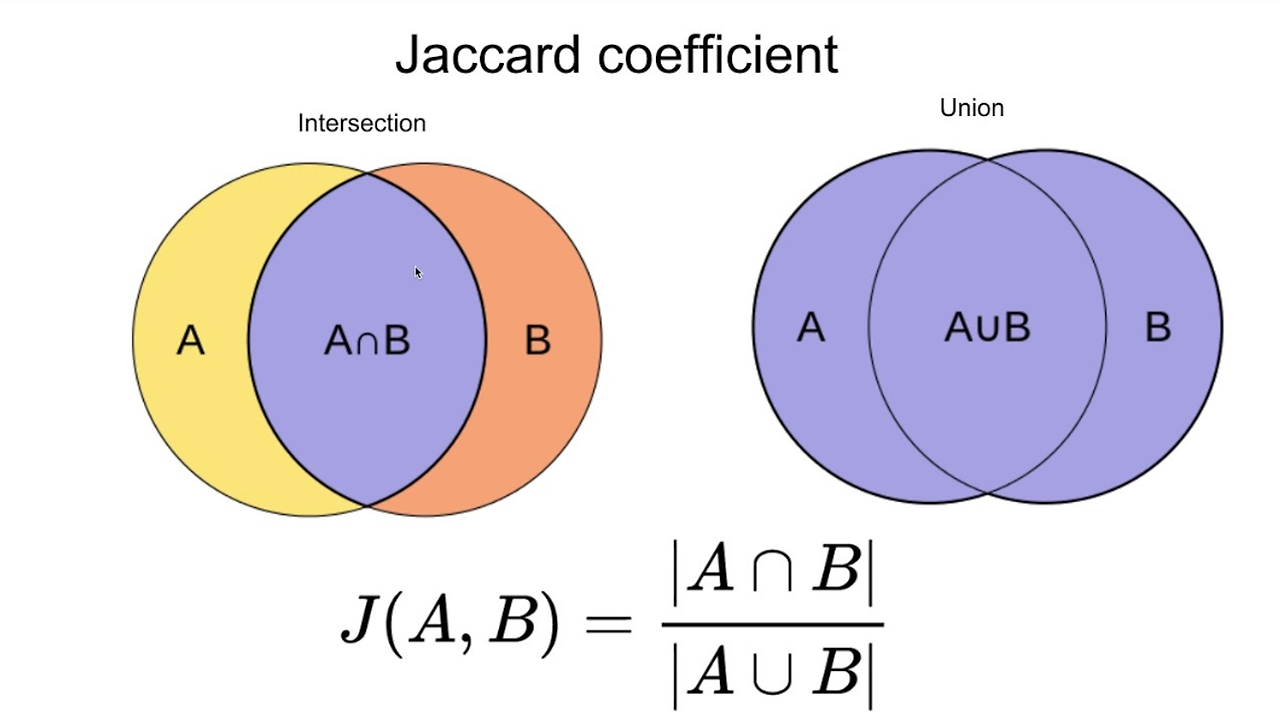
- 두 집합 사이의 유사도를 측정하는 방식으로 주로 텍스트 데이터 대상
- 집합 구성 원소가 같을수록 자카드 유사도가 커지나, 각 집합의 원소 등장 횟수(중복)는 고려 하지 않음
- 주로 두 텍스트 데이터 사이의 유사도를 측정하기 위해 사용
▶ 실습 코드
④ 자카드 스코어
#데이터
lyric1 = "내가 먹고 싶었던 달디 달고 달디 달고 달디 단 밤양갱"
lyric2 = "달디 단 솜사탕 먹고 싶었던 나"
lyric3 = "내가 내가 제일 잘 나가"
lyric1 = lyric1.split()
lyric2 = lyric2.split()
lyric3 = lyric3.split()
# Jaccard similarity 계산 함수
# 계산식: 여집합의 수 / 합집합의 수
# set()는 중복을 없애고 순서가 없는 집합으로 변환해주는 함수.( [] > {} )
# 합집합 union(|), 교집합 intersection(&), 차집합 difference(-), 대칭 차집합 symmetric_difference(^)
# 자카드는 중복의 원소를 고려하지 않으므로 집합 형태로 계산 필요
def jaccard_sim(x1, x2):
a = set(x1)
b = set(x2)
return len(a & b) / len(a | b)
# 상기 return과 같은 결과
# union = a.union(b)
# intersection = a.intersection(b)
# return len(intersection) / len(union)
print(jaccard_sim(lyric1, lyric2)) # 0.4444444444444444
print(jaccard_sim(lyric1, lyric3)) # 0.1
print(jaccard_sim(lyric2, lyric3)) # 0.0
- skelarn 활용
# Scikit-Learn의 jaccard score는 위 계산 방식과 약간 다름
# 데이터를 변형해줘야 함
# https://scikit-learn.org/stable/modules/generated/sklearn.metrics.jaccard_score.html
from sklearn.metrics import jaccard_score
# 토큰화 결과 예시
# tokens = ["내가", "먹고", "싶었던", "달디", "달고", "단", "밤양갱", "솜사탕", "나", "제일", "잘", "나가"]
# l1 = [1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0]
# l2 = [0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0]
# l3 = [1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1]
def jaccard_token(x1, x2, x3):
l1 = []
l2 = []
l3 = []
tokens = list(set(x1 + x2 + x3))
for word in tokens:
if word in x1:
l1.append(1)
else:
l1.append(0)
if word in x2:
l2.append(1)
else:
l2.append(0)
if word in x3:
l3.append(1)
else:
l3.append(0)
return , l2, l3
l1 = jaccard_token(lyric1, lyric2, lyric3)[0] # [1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0]
l2 = jaccard_token(lyric1, lyric2, lyric3)[1] # [0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0]
l3 = jaccard_token(lyric1, lyric2, lyric3)[2] # [1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1]
print(jaccard_score(l1, l2)) # 0.4444444444444444
print(jaccard_score(l1, l3)) # 0.1
print(jaccard_score(l2, l3)) # 0.0'TIL' 카테고리의 다른 글
| [240321] 파이썬: 코드카타 45 & SQL: 코드카타 158~160 (0) | 2024.03.21 |
|---|---|
| [240321] 클러스터링 분석 - ② 차원 축소: 주성분 분석(PCA)과 t-SNE (0) | 2024.03.21 |
| [240319] 스파크(spark): 배경 및 기본 구조, 기능 (1) | 2024.03.19 |
| [240319] 파이썬: 코드카타 44 & SQL: 코드카타 156~157 (0) | 2024.03.19 |
| [240318] 스파크(spark): 병렬/분산처리, 샘플링, 분할, Dask, 자동화 (3) | 2024.03.18 |

