[파이썬으로 하는 클러스터링 분석 by 강민구 튜터]
1. 주성분 분석(PCA)
1) 정의
- 고차원 데이터의 차원을 축소하는 대표적인 방법 중 하나로 Principal Component Analysis의 약어
- 데이터의 특성(분포)을 최대한 보존하면서 차원을 축소하는 ‘주성분’을 찾아내는 방법
└ 분산(Variance)을 보존하면서 서로 직교하는 새 축을 찾아 고차원 공간 표본을 선형 연관성 없는 저차원 공간으로 변환하는 기법
└ 하기 그래프에서는 C1선이 가장 데이터를 잘 담아내는 새로운 차원이 됨

- PCA에서 핵심은 어디서 바라봐야 나무 블록을 가장 잘 볼 수 있을지, 새로운 관점(새로운 차원 aka 주성분)을 찾아내는 것

- 주성분 분석은 기존 변수를 선형 결합해 새로운 변수를 생성하는 변수 추출Feature Extraction 기법 활용
└ 이때 일부가 아닌 모든 차원의 변수들을 사용해서 선형 결합
└ 선형 결합: c1 = a * x1 + b * x2 ( x1 = 차원1, x2 = 차원2 )
- 요약하면, 기존 데이터 차원(feature)값을 결합해 데이터를 잘 설명할 수 있는 새로운 종합 점수(주성분)을 만들어 보다 적은 차원으로 데이터를 설명하려는 방법
2) 주성분 분석 진행 과정

① 데이터의 분산을 최대한 보존하면서 직교하는 새로운 축(기저)을 찾아냅니다.
└ (선형대수) 공분산 행렬의 고유값 분해를 통해 얻어낼 수 있습니다.
② 첫번째 축과 직교(독립)하면서 분산이 최대인 두번째 축을 찾습니다.
③ 위의 방식을 기존 차원만큼 반복합니다.
└ 이렇게 하면 기존 차원의 수 만큼 주성분을 찾아낼 수 있습니다.
④ 주성분이 데이터의 분산을 얼마나 반영하는지 확인하면서 적당한 수의 주성분을 선택합니다.
└ 파이썬에서는 pca_scree.explained_variance_ratio_ 로 분산 반영 비중 확인 가능
└ 기존 분산의 80~90% 이상을 반영하는 최소한의 차원 갯수를 선택합니다.
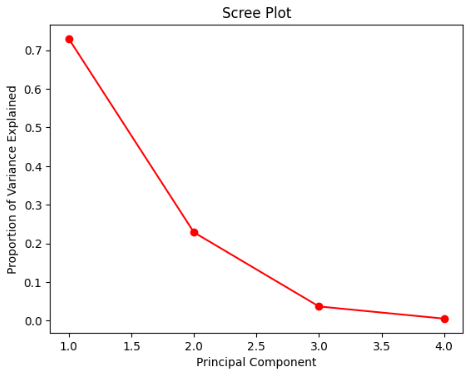
└ 또는 scree plot*을 활용해 elbow point에 해당하는 차원 갯수를 선택합니다.
* 가로축을 차원의 갯수, 세로축을 고유값(eigenvalue, 얼만큼의 분산을 가지고 있는지)으로 만든 plot
* elbow point(팔꿈치처럼 딱 꺽이는 지점)에 있는 2를 주성분(차원)의 개수로 선택하는 것!

⑤ 새로운 차원에 대해 데이터를 사영(좌표변환)해줍니다.
└ 예: c1 = a * x1 + b * x2
3) 주성분 분석의 결과 해석

- 데이터 거리나 분포가 잘 유지되면 차원 축소가 효과적이므로, 주성분 분석이 유용
└ 반면 어느 방향에서 봐도 데이터 분포가 똑같은 데이터는 차원 축소 효과를 기대하기 어려움
: ex. 상관 관계가 없는 데이터의 경우 새로운 차원이 원형 형태로 나와서 의미를 찾기 힘들 것
- 새로운 차원이나 각각의 차원에 대한 해석이 어려울 수 있어 분석 결과 해석에 고민이 필요
└ (예시) 국어, 수학, 사회, 과학 과목에 대한 시험점수(4차원)를 2개 차원으로 축소했을 때,
· c1 = 1.2*국어 + 0.1*수학 + 0.93*사회 + 0.35*과학 → 문과 점수
· c2 = 0.2*국어 + 1.3*수학 + 0.21*사회 + 0.87*과학 → 이과 점수
: 문과/이과로 나눌 수 도 있지만, 축소한 차원으로 묶기 어려운 경우도 있음
· c1 = 1.2*국어 + 2.1*수학 + 1.03*사회 + 0.35*과학 → ???
· c2 = 0.3*국어 + 1.01*수학 + 0.71*사회 + 2.13*과학 → ???
- 하지만 클러스터링에서는 데이터의 분포만 잘 유지되면 PCA를 통한 차원 축소가 효과적
└ 클러스터링은 각각 축이 갖는 의미보다는 '거리'가 중요하기 때문
4) 주성분 분석의 장단점
① 장점
- 고차원의 데이터를 차원 축소하여 데이터 분포를 좀 더 쉽게 살펴볼 수 있음
- 차원 축소를 통해 머신러닝 모델 학습 효율 개선 (차원의 저주 해소)
- 기존 데이터 차원에서의 변수 중요도 확인 가능
└ 주성분으로 선형변환하는 식에서 계수값이 큰 변수는 데이터의 분포에 영향력이 큰 것으로 해석
② 단점
- 기존 차원별 의미와 각 주성분이 어떤 의미(특징값)인지 해석이 어려움
- 데이터의 전체 분포(분산)를 반영한 것이 아니기 때문에 정보 손실 발생
▶ 실습 코드 - PCA
① 라이브러리 및 데이터 불러오기
# 라이브러리 불러오기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
# iris 데이터 불러와서 DataFrame으로 저장
data_iris = datasets.load_iris()
df_iris = pd.DataFrame(data = data_iris.data, columns=data_iris.feature_names) #데이터 프레임
display(df_iris.head(5))
label_iris = data_iris.target #배열
print(label_iris[:5])
② PCA
## iris 데이터 표준화로 스케일링
# 스케일러 불러오기
scaler = StandardScaler()
# split로 칼럼명에서 ' (cm)' 빼기
column_s = [i.split(' (cm)')[0] for i in df_iris.columns]
# ['sepal length', 'sepal width', 'petal length', 'petal width']
# 스케일링하여 새로운 데이터 프레임 생성 (with list comprehension)
# fit_transfor()은 배열을 반환하므로 DataFrame 처리
df_iris_s = pd.DataFrame(data=scaler.fit_transform(df_iris), columns=column_s)
df_iris_s.head(5)
## 정규화된 데이터 대상으로 PCA 진행
# https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html
pca = PCA(n_components=2) # 축소할 주성분의 개수 지정(2차원)
df_iris_pca = pd.DataFrame(data=pca.fit_transform(df_iris_s), columns=['pc1', 'pc2'])
df_iris_pca['label'] = label_iris # target 추가
df_iris_pca.head(5)
## PCA 결과가 분산을 얼마나 보존하고 있는지 확인
pca.explained_variance_ratio_
# array([0.72962445, 0.22850762])
# 2개 차원 분산의 합이 80~90%를 반영하면 결과가 유의미
## 기존 변수들의 선형 관계가 PC(주성분)에서 어떻게 나타나는지 확인
# 'components_'는 주성분 벡터(방향)
pca.components_
print("components_: {}".format(pca.components_))
# 선형 관계 확인
[np.dot(pca.components_[0], df_iris_s.iloc[0]), np.dot(pca.components_[1], df_iris_s.iloc[0])]
df_iris_pca.iloc[0].to_list()
print("선형 관계(np.dot): {}".format([np.dot(pca.components_[0], df_iris_s.iloc[0]), np.dot(pca.components_[1], df_iris_s.iloc[0])]))
print("선형 관계(pca): {}".format(df_iris_pca.iloc[0].to_list()))
[ 선형관계 확인 결과 ]
components_: [[ 0.52106591 -0.26934744 0.5804131 0.56485654]
[ 0.37741762 0.92329566 0.02449161 0.06694199]]
선형 관계(np.dot): [-2.2647028088075905, 0.48002659652098656]
선형 관계(pca): [-2.2647028088075922, 0.4800265965209895, 0.0]
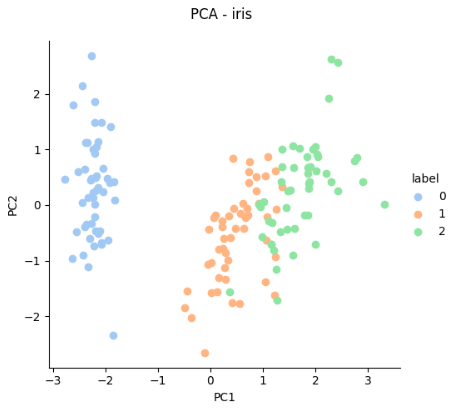
③ PCA 시각화
# PCA 시각화 with Seaborn
g = sns.FacetGrid(df_iris_pca, hue = 'label', height = 5, margin_titles = True,
palette = sns.color_palette('pastel', 3))
g.map_dataframe(plt.scatter, 'pc1', 'pc2')
# 범례 추가
g.add_legend()
# subplot과 간격 조정
g.figure.subplots_adjust(top=0.9)
g.figure.suptitle('PCA - iris')
# x축, y축 이름 지정
g.set_xlabels('PC1')
g.set_ylabels('PC2')
# Scree Plot 그리기
# Scree plot: 가로축을 차원의 갯수, 세로축을 고유값(eigenvalue)으로 만든 plot
# 원본 칼럼의 개수
n_feature = len(df_iris_s.columns)
# 원본 차원 수에 맞춰 PCA 진행
pca_scree = PCA(n_components = n_feature)
pca_scree.fit(df_iris_s)
# pca_scree.n_components_ pca 후 차원의 개수 # 4
# 1부터 시작하도록 +1 추가
pc_arr = np.arange(pca_scree.n_components_) + 1 # array([1, 2, 3, 4])
# x축이 원본과 개수가 동일한 pca 차원의 수, y축은 분산 비율
# pca_scree.explained_variance_ratio_ 값인 array([0.72962445, 0.22850762, 0.03668922, 0.00517871]) 다 더하면 1
plt.plot(pc_arr, pca_scree.explained_variance_ratio_, 'ro-') #'ro-' 빨간색, 표식 추가
plt.title('Scree Plot')
plt.xlabel('Principal Component')
plt.ylabel('Proportion of Variance Explained')
plt.show()
2. t-SNE
1) t-SNE 정의

- 고차원의 데이터를 차원 축소하여 시각화할 때 많이 사용하는 방법
- t-SNE는 t-distributed Stochastic Neighbor Embedding의 약어
└ SNE: 고차원 데이터에 대해 각 데이터 사이 ‘거리’를 최대한 보존하는 방식으로 차원 축소
└ 저차원의 데이터 분포가 t분포를 따르도록 하기 때문에 t-SNE라고 부름
2) t-SNE의 특징
- 고차원에서 거리가 가까운 데이터를 차원 축소 후에도 가까운 곳에 위치 시킴
- 또한 멀리 있는 데이터에 대해서도 신경을 써서 배치
- 어떠한 데이터에 대해서도 꽤 괜찮은 임베딩 결과를 만들어 내(robustness) 클러스터링 시각화에 자주 사용
└ 임베딩(embedding): 데이터를 특정 차원의 벡터로 나타내는 과정 및 결과물
- scikit-learn에서 쓰이는 perplexity(PPL) 하이퍼 파라미터가 차원 축소 결과에 큰 영향을 미침
└ perplexity는 언어 모델을 평가할 때 자주 언급되는 지표로 '2 ** entropy' 로 정의
└ perplexitry를 크게 잡으면, 데이터간 거리가 멀리 떨어진 형태로 무분별하게 찍혀서 결과 해석이 어려움
└ (cf) 엔트로피entropy(정보량)가 크다 = 정보량이 많다 = 일어날 수 있는 가짓수가 많다
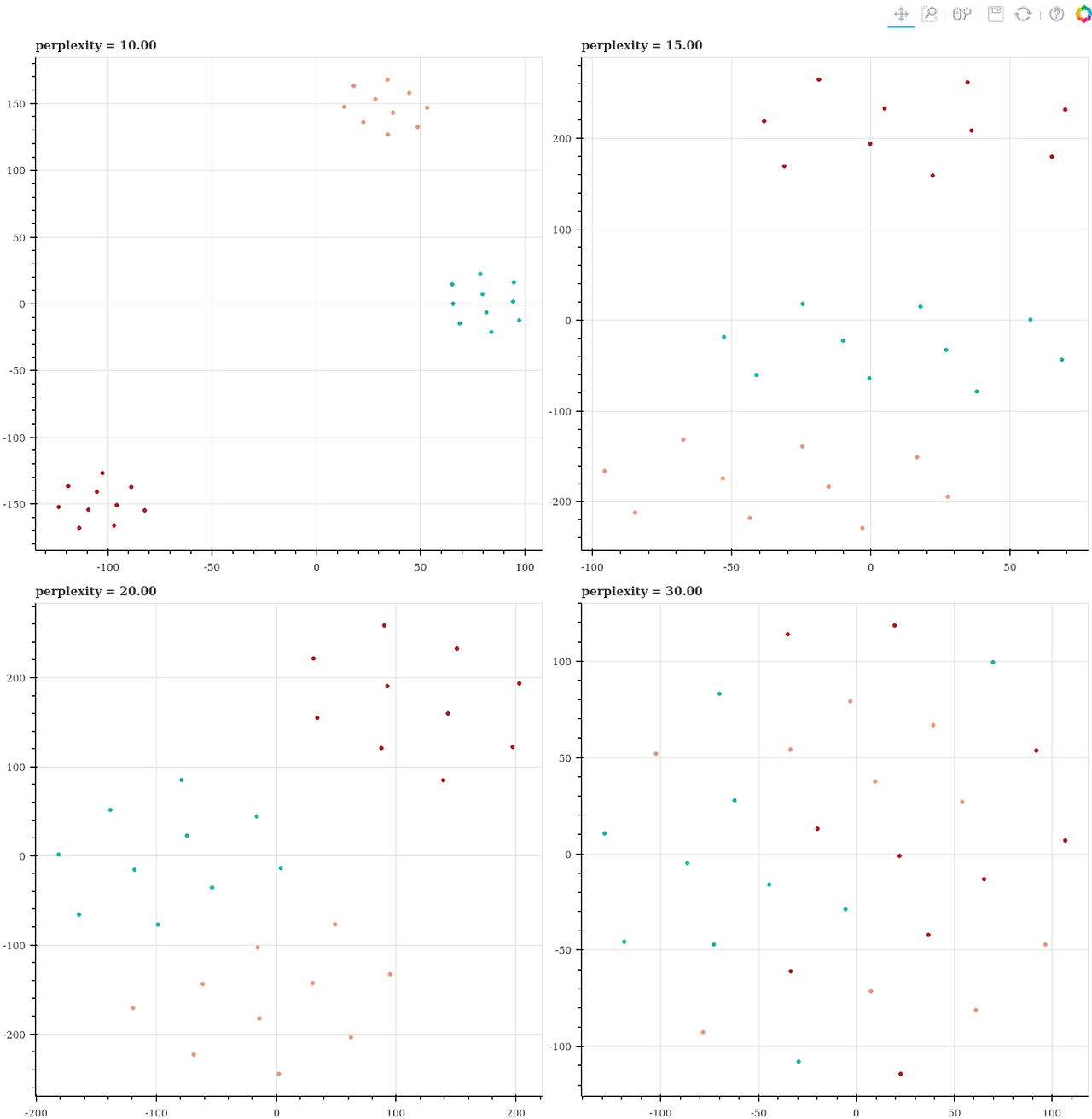
출처 - https://lovit.github.io/nlp/representation/2018/09/28/tsne/
▶ 실습 코드 - t-SNE
① 데이터 확인
# digits 데이터 호출
data_digits = datasets.load_digits()
df_digits = pd.DataFrame(data = data_digits['data'], columns=data_digits['feature_names'])
label_digits = data_digits['target']
print(df_digits.shape)
display(df_digits.head(5))
print(label_digits[:5])
# digits 데이터 이미지 확인
# 전체 이미지 크기 및 간격 설정
# 통상 fig는 바탕 이미지, ax는 subplot으로 생성되는 각 그래프
fig = plt.figure(figsize=(6, 3))
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(8):
# add_subplot 활용: add_subplot(nrows, ncols, index, **kwargs), 열 n개*행 n개의 subplot에 index 위치에 그래프
# fig.add_subplot(1, 8, i+1)는 1열에 8개의 그래프가 들어가는데, for문을 돌면서 한개씩 추가되는 것
# facecolor는 배경색, frameon 프레임 설정 여부 추가 가능
# xticks=[]와 yticks=[]는 x축과 y축의 눈금 제거
ax = fig.add_subplot(1, 8, i+1, xticks=[], yticks=[])
# data_digit에 image라는, 8개열씩 짤린 배열이 저장돼 있음. images[0]은 첫번째 이미지 배열 출력
# ax.imshow()는 이미지를 시각화
# cmap=plt.cm.gray_r은 컬러 맵을 회색조로 이미지 표시
# interpolation='nearest'는 이미지 삽입(interpolation) 방법을 설정
ax.imshow(data_digits.images[i], cmap=plt.cm.gray_r, interpolation='nearest')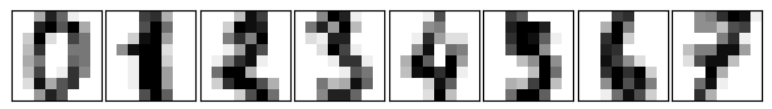
② t-SNE 학습 및 시각화
# t-sne 학습
# https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html
tsne = TSNE(n_components=2)
df_digits_tsne = pd.DataFrame(data = tsne.fit_transform(df_digits), columns=['col1', 'col2'])
df_digits_tsne['label'] = label_digits
df_digits_tsne.head(5)
#t-sne 시각화
t = sns.FacetGrid(df_digits_tsne, hue ='label', height=5, palette = sns.color_palette('Set2') )
# map_datafram(그래프 종류, x축, y축, 기타 설정..)
t.map_dataframe(plt.scatter, 'col1', 'col2', s=10)
# 범례 추가
t.add_legend()
# 타이틀 및 간격, 축 이름 설정
t.figure.suptitle('t-SNE - digits')
t.figure.subplots_adjust(top=0.9)
t.set_xlabels('x')
t.set_ylabels('y')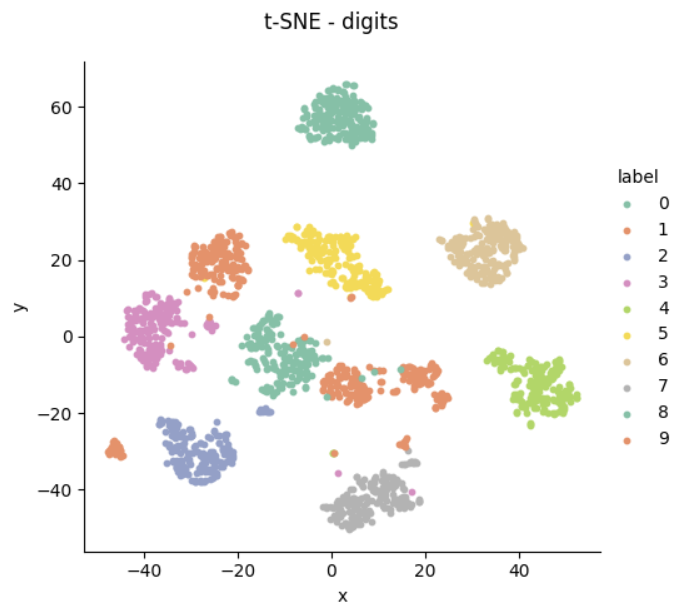
③ PCA로 동일 데이터 시각화
## 동일 데이터를 PCA 시각화하여 결과 비교
# 표준화 진행
scaler_pca = StandardScaler()
df_digits_s = pd.DataFrame(data = scaler_pca.fit_transform(df_digits))
# PCA 진행
pca_digit = PCA(n_components=2)
df_digits_pca = pd.DataFrame(data= pca_digit.fit_transform(df_digits_s),columns=['col1', 'col2'] )
df_digits_pca['label'] = label_digits
df_digits_pca.head(5)
#PCA가 커버하는 분산 확인
pca_digit.explained_variance_ratio_ # array([0.12033916, 0.09561054])
#PCA 결과 시각화
p = sns.FacetGrid(df_digits_pca, hue ='label', height=5, palette = sns.color_palette('Set2'))
# map_datafram(그래프 종류, x축, y축, 기타 설정..)
p.map_dataframe(plt.scatter, 'col1', 'col2', s=10)
# 범례 추가
p.add_legend()
# 타이틀 및 간격, 축 이름 설정
p.figure.suptitle('PCA - digits')
p.figure.subplots_adjust(top=0.9)
p.set_xlabels('x')
p.set_ylabels('y')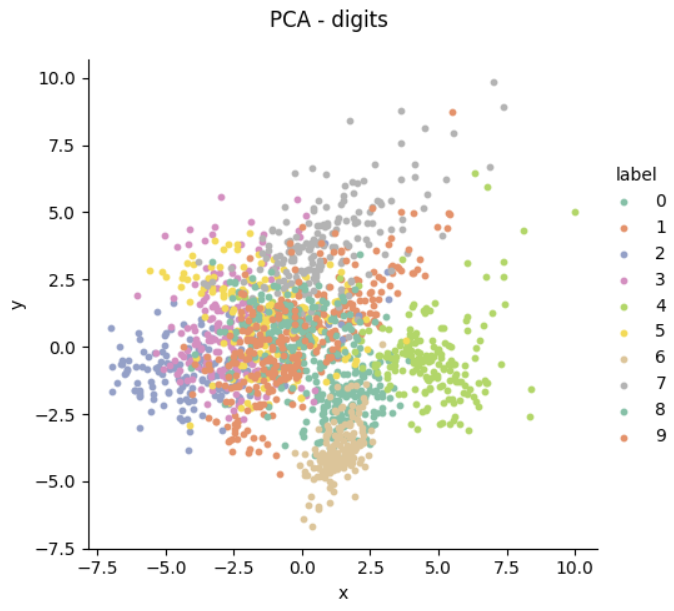
④ t-SNE 3차원으로 시각화
# 3원으로 t-SNE 학습
tsne_3com = TSNE(n_components=3)
df_digits_tsne_3com = pd.DataFrame(data = tsne_3com.fit_transform(df_digits), columns=['col1', 'col2', 'col3'])
df_digits_tsne_3com['label'] = label_digits
df_digits_tsne_3com.head(5)
# t-SNE 3차원으로 시각화
fig = plt.figure(figsize=(12, 9))
t3 = fig.add_subplot(1, 1, 1, projection='3d')
# label(target)별로 데이터를 분리하여 scatter 차트를 각각 그려주기
for i in range(10):
target_3d = df_digits_tsne_3com[df_digits_tsne_3com['label'] == i]
t3.scatter(target_3d['col1'], target_3d['col2'], target_3d['col3'], label = i)
# 타이틀 및 간격, 축 이름 설정
t3.figure.suptitle('t-SNE - digits(3D)')
t3.figure.subplots_adjust(top=1)
t3.set_xlabel('x')
t3.set_ylabel('y')
t3.set_zlabel('z')
# 범례 추가
t3.legend(bbox_to_anchor=(1.1, 0.95))
plt.show()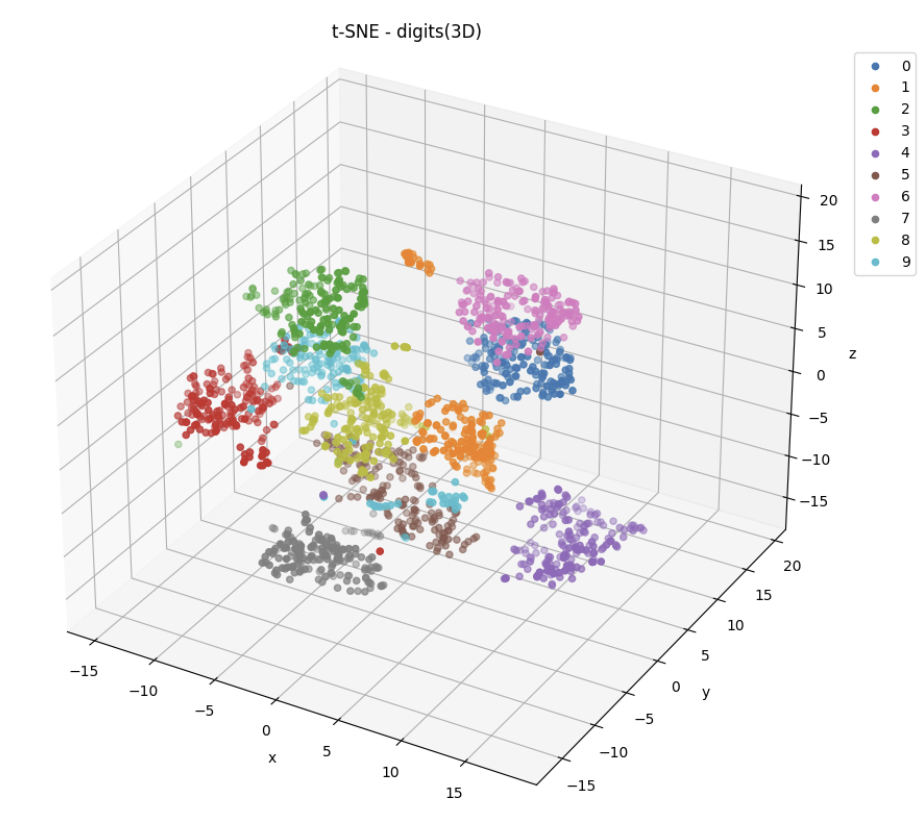
# 라이브러리를 활용한 3D 시각화
# 정답
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import ListedColormap
fig = plt.figure(figsize = (8,8))
ax = Axes3D(fig)
fig.add_axes(ax)
sc= ax.scatter("col1", "col2", "col3",\
data = df_digits_tsne_3d,\
c = df_digits_tsne_3d["label"],\
cmap = ListedColormap(sns.color_palette()))
plt.legend(*sc.legend_elements(), bbox_to_anchor=(1.05, 1), loc=2)
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
(참고) 패싯 그리드 FacetGrid 시각화
1) FacetGrid란?
- 다양한 범주형 값을 가지는 데이터를 시각화하는데 좋은 방법
- 행, 열 방향으로 서로 다른 조건을 적용하여 여러 개의 서브 플롯 제작 가능
- 각 서브 플롯에 적용할 그래프 종류를 map() 메서드를 이용해 그리드 객체에 전달
2) 그리는 방법
① FacetGrid에 데이터프레임과 구분할 row, col, hue 등을 전달해 객체 생성
② 객체(facet)에그릴 그래프의 종류와 종류에 맞는 컬럼을 map 메서드를 활용해 전달
facet = sns.FaceGrid(df, col='sex', row='survived', hue='pclass', size=5)
facet = facet.map(sns.regplot, 'fare', 'age', fit_reg=False)
facet = facet.add_legend()
facet = facet.figure.subplots_adjust(wspace = .05, hspace = .05)
* 참고 Seaborn - 패싯 그리드 : FacetGrid
(부록) 참고자료
- [이기창님의 블로그 - 주성분분석(Principal Component Analysis)]
- [이기창님의 블로그 - t-SNE]
- [lovit님의 블로그 - t-Stochastic Neighbor Embedding (t-SNE) 와 perplexity]
- [블로그 - t-sne의 개념 및 알고리즘 설명]
'TIL' 카테고리의 다른 글
| [240322] 파이썬 실습 코드: 메모리 경량화 (with parquet) (0) | 2024.03.22 |
|---|---|
| [240321] 파이썬: 코드카타 45 & SQL: 코드카타 158~160 (0) | 2024.03.21 |
| [240320] 파이썬으로 하는 클러스터링 분석 - ① 기본 개념과 거리 계산 (0) | 2024.03.20 |
| [240319] 스파크(spark): 배경 및 기본 구조, 기능 (1) | 2024.03.19 |
| [240319] 파이썬: 코드카타 44 & SQL: 코드카타 156~157 (0) | 2024.03.19 |


