[머신러닝의 이해와 라이브러리 활용 심화 by 임정 튜터]
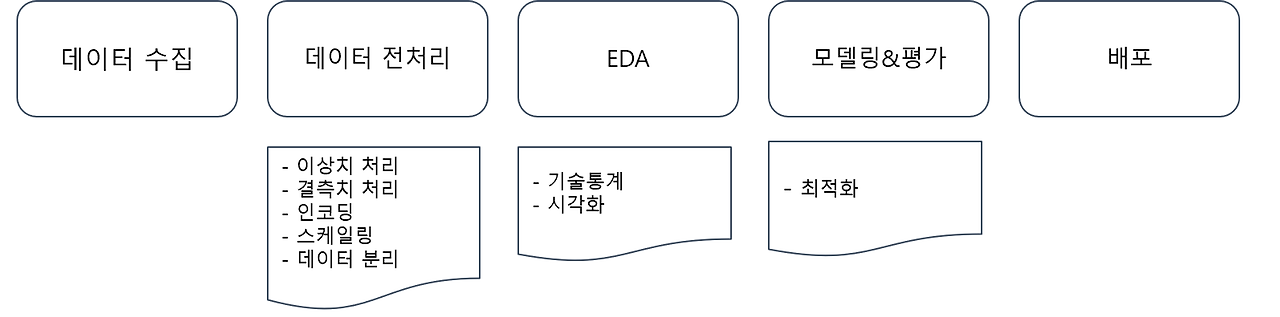
1. 데이터 분석(예측모델링) 프로세스
1) 데이터 수집
▶ 데이터 수집에 따른 프로세스
- 실제 데이터 수집은 개발을 통해 데이터를 적재하고 수집하는 데이터 엔지니어링 역량이 필요
- 주로 데이터 분석가는 이미 존재하는 데이터를 추출해 리포팅 혹은 머신러닝을 통한 예측을 담당
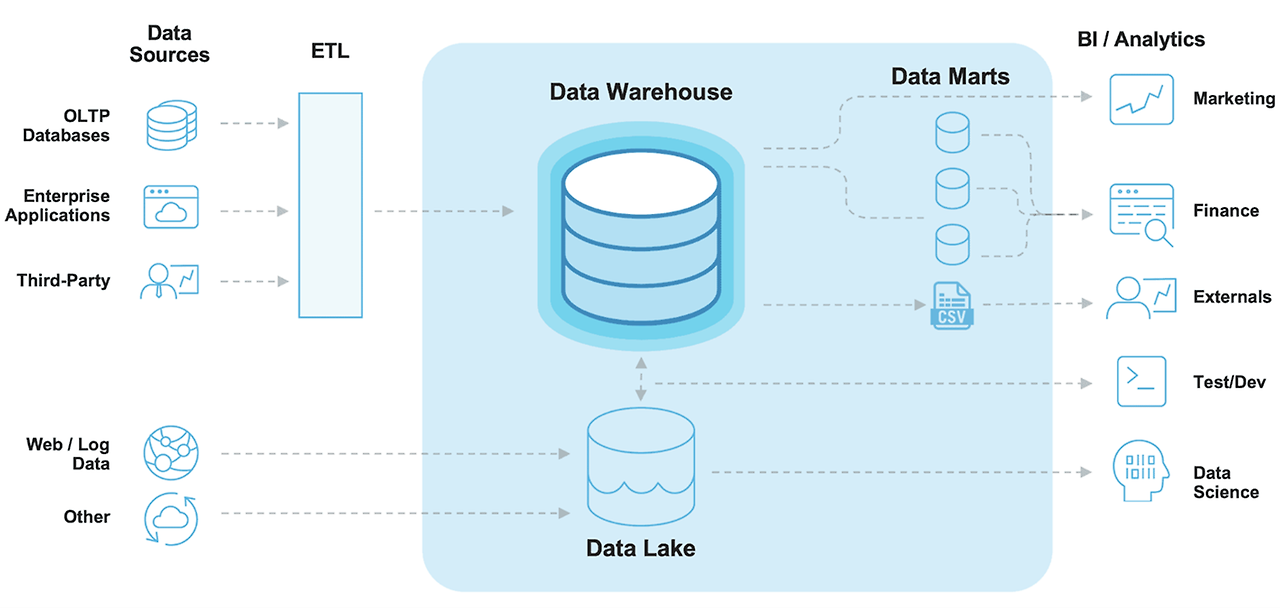
① Data Source
- OLTP Database: 온라인 쇼핑, 주문 등 동시에 발생하는 다수의 트랜잭션(데이터베이스 작업의 단위) 처리 유형
* OnLine Transaction Processing의 약자
- Enterprise Applications: 회사 내 데이터 (ex 고객 관계 데이터, 제품 마케팅 세일즈)
- Third - Party: Google Analytics와 같은 외부소스에서 수집되는 데이터
- Web/Log: 사용자의 로그데이터
> ETL이라는 추출 변환 과정을 통해 Data Warehouse로 이동
② Data Lake: 원시 형태의 다양한 유형의 데이터를 저장
③ Data Warehouse: 보다 구조화된 형태로 정제된 데이터를 저장
④ Data Marts: 회사의 금융, 마케팅, 영업 부서와 같이 특정 조직의 목적을 위해 가공된 데이터
⑤ BI/Analytics: business Intelligence(BI)는 의사결정에 사용될 데이터를 수집하고 분석하는 프로세스
▶ 실제 데이터 수집
- 회사 내 Data가 있다면? SQL 혹은 Python 을 통해 데이터 마트 생성
- 회사 내 Data가 없다면? 데이터 수집 필요 ① 존재하는 데이터 다운로드 ② API를 이용한 데이터 수집 ③ Data Crawling
2) 탐색적 데이터 분석(Exploratory Data Analysis, EDA)
: 데이터의 시각화, 기술통계 등 방법을 통해 데이터를 이해하고 탐구하는 과정
: EDA를 통해 데이터 및 모델링에 대한 정보를 얻을 수 있음
▶ 기술통계를 통한 EDA 예시
- (예시) tips 데이터: tips.describe()
└ include='all' 옵션을 통해 범주형 데이터도 확인 가능(최빈값 확인에 유효)

▶ 시각화를 이용한 EDA 예시
(예시) tips 데이터

① countplot: 범주형 자료의 빈도 수 시각화
- 방법: 범주형의 데이터의 각 카테고리별 빈도수를 나타낼 때 ex. 제품 카테고리별 판매수 파악
- x축: 범주형 자료, y축: 자료의 빈도수
② barplot: 범주형 자료의 시각화
- 방법: 범주형 데이터의 각 카테고리에 따른 수치 데이터의 평균을 비교 ex. 연령대별 평균소득을 비교
- x축: 범주형 자료, y축: 연속형 자료

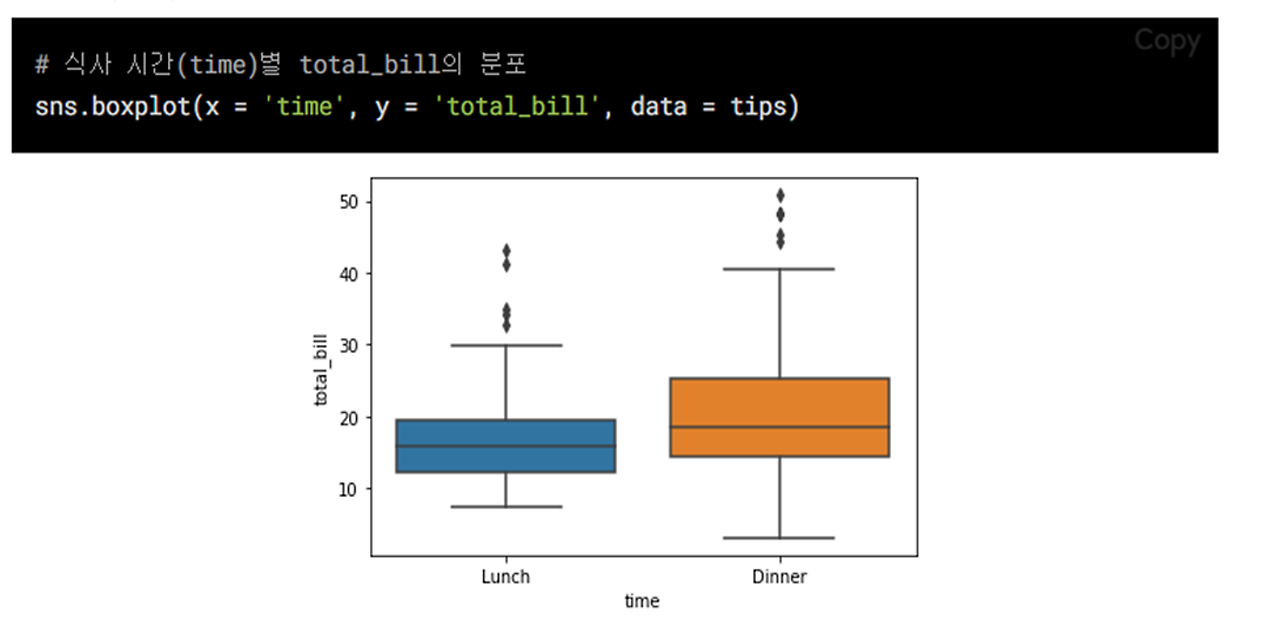
③ boxplot: 수치형 & 범주형 자료의 시각화
- 방법: 데이터의 분포, 중앙값, 사분위 수, 이상치 등을 한눈에 표현하고 싶을 때 ex. 그룹간 시험 점수 분포 비교
- x: 수치형 or 범주형, y: 수치형 자료
④ histogram: 수치형 자료 빈도 시각화
- 방법: 연속형 분포를 나타내고 싶을 때, 데이터가 몰려있는 구간을 파악하기 쉬움 ex. 고객 연령 분포 파악
- x축: 수치형 자료, y축: 자료의 빈도수

⑤ scatterplot: 수치형끼리 자료의 시각화
- 방법: 두 연속형 변수간의 관계를 시각적으로 파악하고 싶을 때 ex. 키와 몸무게 간의 관계
- x축: 수치형 자료, y축: 수치형 자료
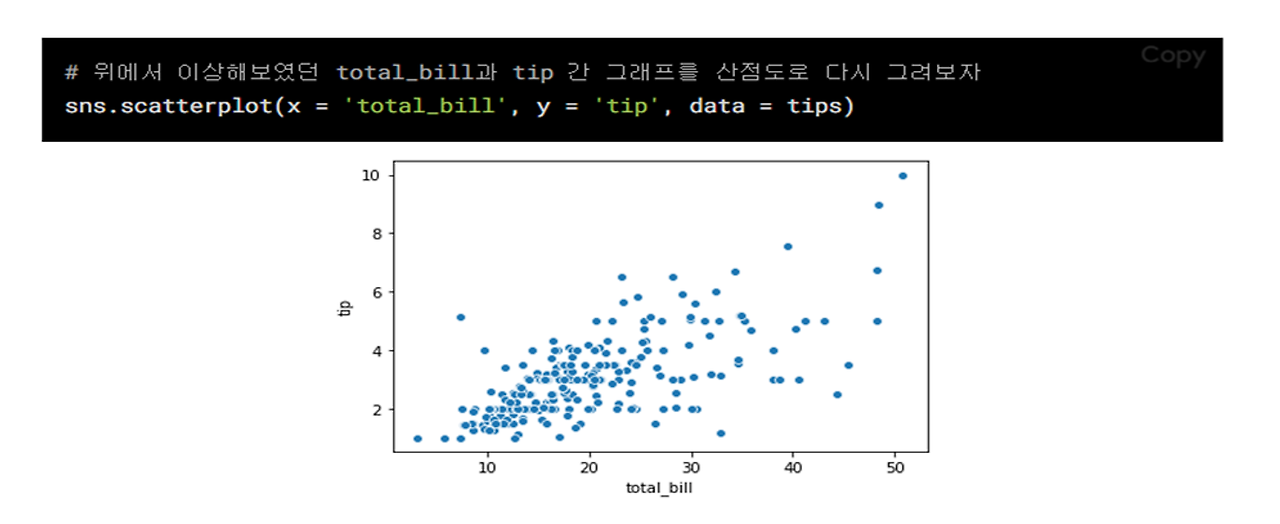
⑥ pairplot: 전체 변수에 대한 시각화
- 방법: 한 번에 여러 개의 변수를 동시에 시각화 하고 싶을 때
- x축: 범주형 or 수치형 자료, y축: 범주형 or 수치형 자료
- 같은 변수가 만났을 때는 히스토그램으로 분포를 그려줌 (대각선 기준으로 밑이나 위에 한 쪽만 보면 됨)
- 모든 변수를 다 만들어서 보여주나 범주형은 제외됨
- 변수가 너무 많으면 출력 시 데이터를 슬라이싱 해서 나눠 봐도 됨
3) 데이터 전처리
: 데이터 전처리는 전체 분석 프로세스에서 90%를 차지 할 정도로 노동, 시간 집약적인 단계
▶ 이상치(Outlier)
: 관측된 데이터 범위에서 많이 벗어난 아주 작은 값 혹은 큰 값
: 이상치는 다소 주관적인 값으로 도메인과 비지니스 맥락에 따라 기준이 상이
: 이상치 삭제 시 데이터 품질은 좋아질 수 있지만 정보 손실을 동반해 처리에 주의가 필요
: 다른 데이터 패턴을 보이는 개체/자료를 찾는 이상 탐지(Anomaly Detection)로 발전 가능 ex.사기탐지, 사이버보안 등
① Extreme Studentized Deviation(ESD) 이용한 이상치 발견

- 데이터가 정규분포를 따른다고 가정할 때, 평균에서 표준편차의 3배 이상 떨어진 값
└ 좌우측의 값을 모두 더해서 이상치 값이라고 가정
- 모든 데이터가 정규 분포를 따르지 않을 수 있기 때문에 다음 상황에서는 제한됨
└ 데이터가 크게 비대칭일 때( → Log변환 등을 노려볼 수 있음)
└ 샘플 크기가 작을 경우
- (실습) 이상치 확인 코드
import numpy as np
mean = np.mean(tips_df['total_bill'])
std = np.std(tips_df['total_bill'])
upper_limit = mean + 3*std # 46.43839435626422
lower_limit = mean - 3*std # -6.866509110362578
② IQR(Inter Quantile Range)를 이용한 이상치 발견
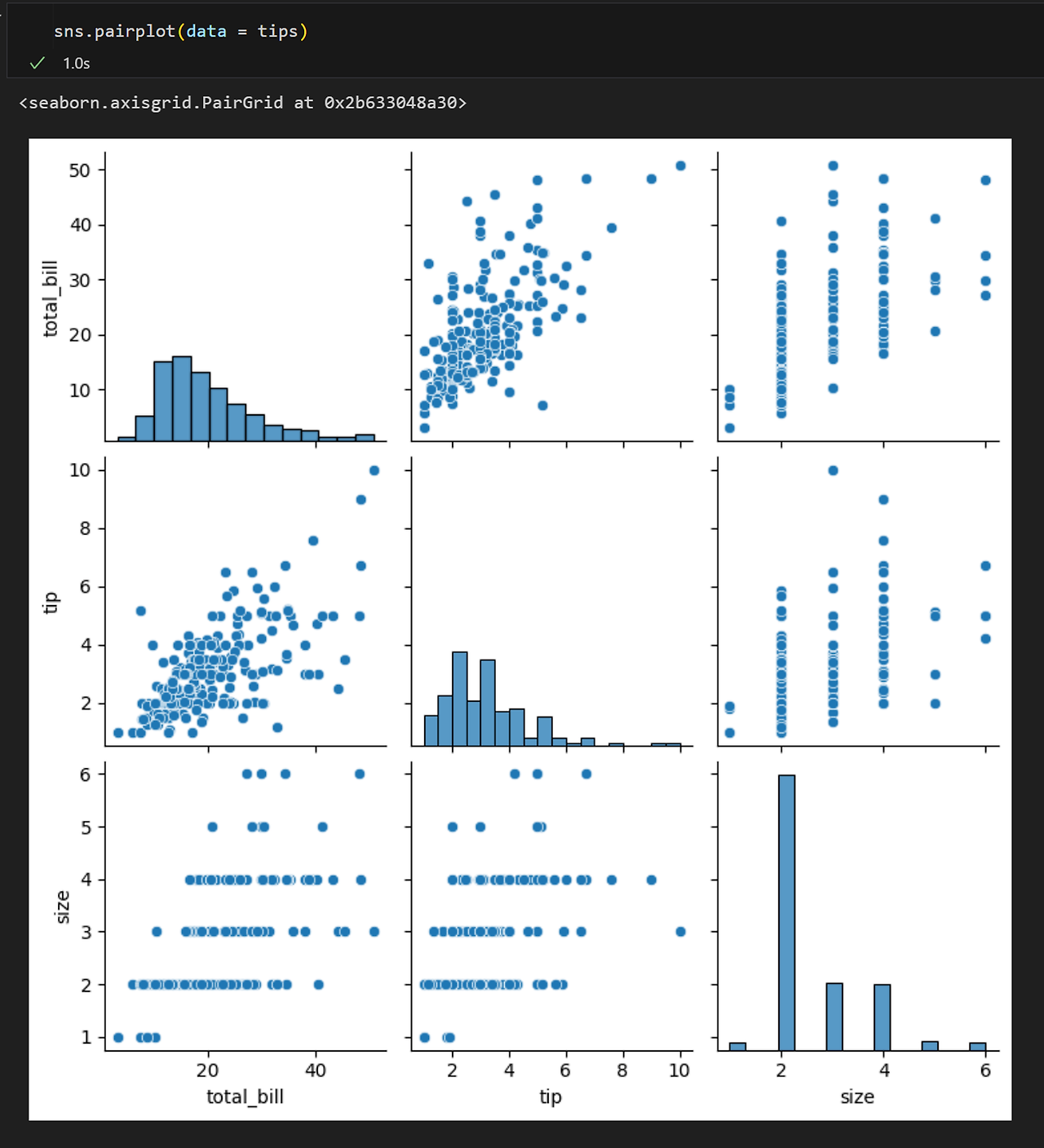
- ESD와 동일하게 데이터가 정규분포라고 가정하고, 비대칭적이거나 샘플사이즈가 작은 데이터는 제한됨
- IQR은 전체 데이터의 25%~75%로 Box plot의 박스 영역에 해당
└ 데이터를 순서에 따라 4등분한 것을 사분위 수라고 하며, Q1~4로 나뉨
└ 박스 최하단이 Q1(25%), 박스 내 선이 Q2(50%, 중위수), 박스 최상단이 Q3(75%)
└ 식으로 표현하면 IQR = Q3 - Q1
- IQR로 이상치 구하는 법
$$ 상한 \ 이상치 = Q3 + 1.5*IQR \\ 하한 \ 이상치 = Q1 - 1.5*IQR $$
- (실습) 이상치 확인 코드
Q1 = tips_df['total_bill'].quantile(0.25)
Q3 = tips_df['total_bill'].quantile(0.75)
IQR = Q3 - Q1
uppper_limit = Q3 + 1.5*IQR # 46.43839435626422
lower_limit = Q1 - 1.5*IQR # -2.8224999999999945
(실습) 이상치 처리 방법
- 삭제 (다른 데이터도 없어지므로 고려 필요)
└ 조건필터링을 통한 삭제(a.k.a. boolean Indexing): df[ df['column'] > limit_value]
# 이상치 조건 적용
cond = (tips_df['total_bill'] > upper_limit) | (tips_df['total_bill'] < lower_limit)
# 데이터프레임[boolean]을 넣으면, True인 값만 나옴!
tips_df[cond]
# boolean 타입앞에 ~ 표시하면 False와 True 반전되면서 이상치 제외 값만 출력됨
tips_df[~cond]
# 데이터 프레임에 입히면 삭제
tips_df = tips_df[~cond]
- 상한/하한 이상치로 대체
# 이상치 조건 적용
cond = (tips_df['total_bill'] > upper_limit) | (tips_df['total_bill'] < lower_limit)
# 함수 생성하여 이상치는 상/하한치로 일괄 적용
def get_limit(x):
if x > upper_limit:
return upper_limit
elif x < lower_limit:
return upper_limit
else:
return x
tips_df['total_bill_en'] = tips_df['total_bill'].apply(get_limit)
tips_df[cond]
▶ 결측치(Missing Value)
: 존재하지 않는 데이터
- 결측치 처리 방법
└ 수치형 데이터
· 평균값 대치: 대표적인 대치 방법
· 중앙값 대치: 데이터에 이상치가 많아 평균 값이 대표성이 없다면 중앙 값 이용 ex) 이상치는 평균 값을 흔들리게 함
└ 범주형 데이터
· 최빈값 대치
- 사용 함수
└ 간단한 삭제 & 대치
· df.dropna(axis = 0): 행 삭제
· df.dropna(axis = 1): 열 삭제
· df.fillna(value)`: 특정 값으로 대치(평균, 중앙, 최빈값)
└ 알고리즘을 이용 (Imputation라는 방법론)
· sklearn.impute.SimpleImputer:평균, 중앙, 최빈값으로 대치
> SimpleImputer.statistics_: 대치한 값 확인 가능
· sklearn.impute.IterativeImputer: 다변량대치(회귀 대치). 결측치(y변수)를 다른 데이터를 활용해 예측하는 것
· sklearn.impute.KNNImputer: KNN(K-Nearest Neighbors, k 최근접 이웃) 알고리즘을 이용한 대치. 주변 정보를 통해서 성질을 알아보는 것
- (실습) 결측치 처리 코드
#titanic 데이터 활용
titanic_df.info() # 결측치 확인
# 전체 결측치 삭제 - dropna
# 중복되는 모든 결측치 삭제되어서 대부분 날라감
titanic_df.dropna(axis=0).info()
# 원하는 결측치만 삭제 - isna() / notna()
# 결측치 여부에 따른 boolean 설정 후 na아닌 값만 출력
titanic_cond = (titanic_df['Age'].notna())
titanic_df = titanic_df[titanic_cond]
# 결측치 대치 - fillna
# fillna엔 단일 값만 들어가야
age_mean = titanic_df['Age'].mean().round(2)
titanic_df['Age_en'] = titanic_df['Age'].fillna(age_mean)
## SimpleImputer를 이용한 대치
## 기본 대치 값은 mean
from sklearn.impute import SimpleImputer
si = SimpleImputer()
# 적합 진행 # Serise로 넣어줘야 함 [[]]
si.fit(titanic_df[['Age']])
# 대치 값 확인
si.statistics_ # array([29.69911765])
# 대치 값 적용
si.transform(titanic_df[['Age']]) # array([[22. ], ... [32. ]])
titanic_df['Age_si'] = si.transform(titanic_df[['Age']])
▶ 범주형 데이터 전처리 - 인코딩(Encoding)
: 인코딩의 사전적 뜻은 어떤 정보를 정해진 규칙에 따라 변환하는 것. 머신러닝에선 숫자로 변환해주는 과정
① 레이블 인코딩(Label Encoding)
- 정의: 문자열 범주형 값을 순서에 맞춰 고유한 숫자로 할당. 각 범주의 크기 및 값의 방향성이 같으면 됨
└ ex. 1등급 → 0 / 2등급 → 1 / 3등급 → 2
- 특징
└ 장점: 모델이 처리하기 쉬운 수치형으로 데이터 변환
└ 단점: 실제로는 그렇지 않은데, 순서 간 크기에 의미가 부여되어 모델이 잘못 해석 할 수 있음
- 사용 함수
: sklearn.preprocessing.LabelEncoder
└ 메소드
· fit: 데이터 학습
· transform: 정수형 데이터로 변환
· fit_transform: fit과 transform을 연결하여 한 번에 실행
· inverse_transform: 인코딩된 데이터를 원래 문자열로 변환
└ 속성
· classes_: 인코더가 학습한 클래스(범주) ex. 학점이면 A, B ...F가 뜸
② 원-핫 인코딩(One-Hot Encoding)
- 정의: 각 범주를 이진 형식으로 변환하는 기법 (각 위치를 1로 정하는 것)
└ 빨강 → [1,0,0] / 파랑 → [0,1,0] / 초록 → [0,0,1]
- 특징
└ 장점: 각 범주가 독립적으로 표현되어, 순서가 중요도를 잘못 학습하는 것을 방지, 명목형 데이터에 권장
└ 단점: 범주 개수가 많을 경우 차원이 크게 증가(차원의 저주) , 모델의 복잡도 증가, 과적합 유발
- 사용 함수
: pd.get_dummies (원-핫인코딩을 더미한다고 함)
: sklearn.preprocessing.OneHotEncoder
└ 메소드(LabelEncoder와 동일)
· categories_: 인코더가 학습한 클래스(범주)
· get_feature_names_out()`: 학습한 클래스 이름(리스트)
(실습) 인코딩
# 함수 불러오기
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
le = LabelEncoder()
oe = OneHotEncoder()
## 라벨인코더
# 모델 학습
le.fit(titanic_df[['Sex']])
# 클래스 확인
le.classes_ #array(['female', 'male']
# 인코딩 진행
le.transform(titanic_df[['Sex']])
titanic_df['sex_le'] = le.transform(titanic_df[['Sex']])
## 원핫인코더
# 모델 학습
oe.fit(titanic_df[['Embarked']])
# 카테고리 확인
oe.categories_ #[array(['C', 'Q', 'S', nan]
# 인코딩 진행
oe.transform(titanic_df[['Embarked']])
# <891x4 sparse matrix of type '<class 'numpy.float64'>'
# 해석: 891 x 4 는 891의 행에 4개의 카테고리(C, Q, S, nan)로 알아서 변경했다는 의미
# with 891 stored elements in Compressed Sparse Row format>
# 해석: Compressed Sparse Row(CSR) 압축된 희소행으로 sparse matrix와 비슷한 의미
# CSR(Compressed Sparse Row) 데이터 데이터프레임으로 만들기
embarked_csr = oe.transform(titanic_df[['Embarked']])
embarked_csr_df = pd.DataFrame(embarked_csr.toarray(), columns= oe.get_feature_names_out())
# 원본 데이터에 원핫인코딩 내용 붙이기
pd.concat([titanic_df, embarked_csr_df], axis=1)
▶ 수치형 데이터 전처리 - 스케일링(Scaling)
: 인코딩이 범주형 전처리라면, 스케일링은 수치형 자료에 대한 전처리.
: 머신러닝의 학습에 사용되는 데이터는 서로 단위 값이 다르기 때문에 이를 보정하는 것
① 표준화(Standardization)
- 각 데이터에 평균을 빼고 표준편차를 나누어 평균을 0 표준편차를 1로 조정하는 방법
- 수식
$$ x_{new} = \frac{x-x_{mean}}{x_{std}} $$
* cf. 표준 편차 구하기: 1,2,3,4,5 / 편차는 각 값에서 평균(3)을 뺀 값을 제곱해서 더함 > 루트 씌운 값. √10 = 3.3
└ [ 1,2,3,4,5 ] 예시:[(1 - 3 / 3.3 = -0.6), (2 - 3 / 3.3 = -0.3), (3 - 3 / 3.3 = 0), (4 - 3 / 3.3 = 0.3), (5 - 3 / 3. 1 - 3 / 3.3 = -0.6)]
· 상기 수식을 진행하면 가운데는 평균은 무조건 0이 되고, 정규분포 형태로 변함
- 함수: sklearn.preprocessing.StandardScaler
└ 메소드
· fit: 데이터학습(평균과 표준편차를 계산)
· transform: 데이터 스케일링 진행
└ 속성
· mean_: 데이터의 평균 값
· scale_, var_: 데이터의 표준 편차,분산 값
· n_features_in_: fit 할 때 들어간 변수 개수
· feature_names_in_: fit 할 때 들어간 변수 이름
· n_samples_seen_: fit 할 때 들어간 데이터의 개수
- 특징
└ 장점
· 이상치가 있거나 분포가 치우쳐져 있을 때 유용
· 모든 특성의 스케일을 동일하게 맞춤. 많은 알고리즘에서 좋은 성능을 가짐
└ 단점
· 데이터의 최소-최대 값이 정해지지 않음
② 정규화(Normalization)
- 정의: 데이터를 0과 1사이 값으로 조정(최소값 0, 최대값 1)
- 수식:
$$ x_{norm} = \frac{x-x_{min}}{x_{max}-x_{min}} $$
└ [ 1,2,3,4,5 ] 예시: 1 : 0, 2: (2-1/5-1 = 0.25), 3: (3-1/5-1 = 0.50), 4: (4-1/5-1 = 0.75), 5 : 1
- 함수: sklearn.preprocessing.MinMaxScaler
└ 속성
· data_min_: 원 데이터의 최소 값
· data_max_: 원 데이터의 최대 값
· data_range_: 원 데이터의 최대-최소 범위
- 특징
└ 장점
· 모든 특성의 스케일을 동일하게 맞춤
· 최대-최소 범위가 명확
└ 단점:
· 이상치에 영향을 많이 받을 수 있음(반대로 말하면 이상치가 없을 때 유용)
: 이상치가 있으면 중간에 값이 붕 뜨게 (ex. [1,2,3,10000] 이면 중간에 값이 크게 빔)
③ 로버스트 스케일링(Robust Scaling)
- 정의: 중앙값과 IQR을 사용하여 스케일링.
- 수식
$$ x_{robust} = \frac{x-median}{IQR} $$
- 함수: sklearn.preprocessing.RobustScaler
└ 속성
· center_: 훈련 데이터의 중앙값
- 특징
└ 장점: 이상치의 영향에 덜 민감
└ 단점: 표준화와 정규화에 비해 덜 사용됨
(실습) 스케일링
# EDA를 통해 스케일링 방법 결정
import seaborn as sns
sns.pairplot(data=titanic_df[['Age', 'Fare']])
titanic_df[['Age', 'Fare']].describe()
# age는 minmax(정규화)로 하고, fare는 standardscaler(표준화)가 적합할 것으로 보임
from sklearn.preprocessing import MinMaxScaler, StandardScaler
sd_sc = StandardScaler()
mm_sc = MinMaxScaler()
titanic_df['Fare_sd_sc'] = sd_sc.fit_transform(titanic_df[['Fare']])
titanic_df['Age_mean_mm_sc'] = mm_sc.fit_transform(titanic_df[['Age_en']])
# 결과 그래프로 확인
sns.histplot(titanic_df['Fare_sd_sc'])
sns.histplot(titanic_df['Age_mean_mm_sc'])
4) 데이터 분리
▶ 머신러닝의 적, 과적합이란?
- 정의
: 과대적합(Overfitting)은 국소적인 문제 해결에 집중한 나머지 일반적인 문제를 해결하지 못하는 현상
: 데이터를 너무 과도하게 학습한 나머지 해당 문제만 잘 맞추고 새로운 데이터를 제대로 예측 혹은 분류하지 못하는 현상
: 과소적합(Underfitting)은 과대적합의 반대로 제대로 학습이 부족해 제대로 예측 및 분류하지 못하는 것
(쉬운 예시) 고3이 3월 모의고사만 열-심히 공부하고 수능을 치르는 것: 3월 모의고사에는 고3 수업과정이 미포함!
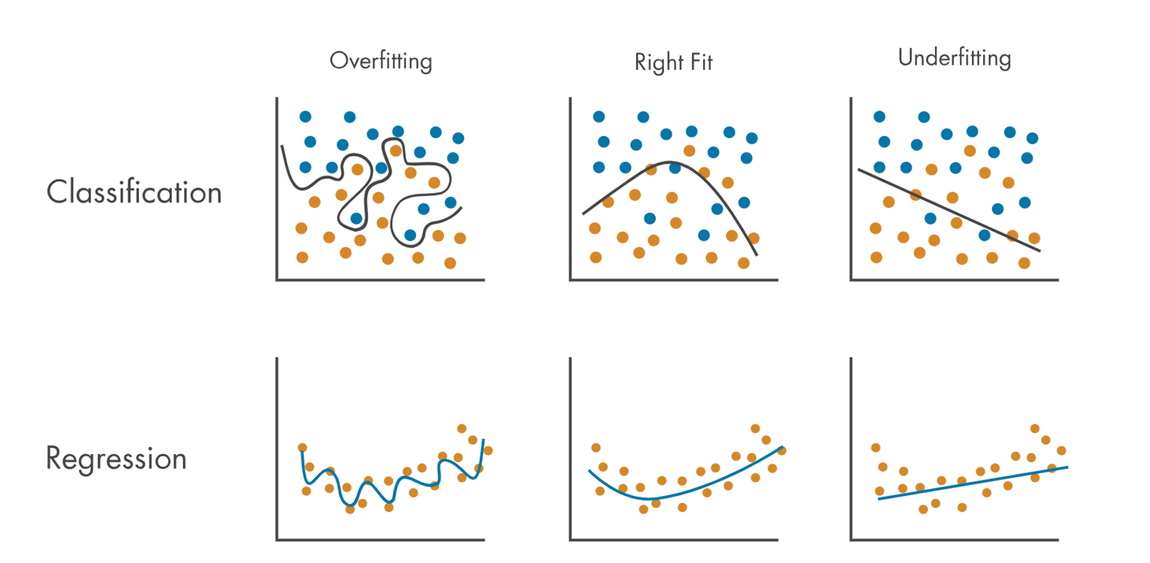
- 과적합의 원인
① 모델의 복잡도
└ 모형이 지나치게 복잡할 때 : 과대 적합이 될 수 있음
└ 모형이 지나치게 단순할 때: 과소 적합이 될 수 있음
② 데이터 양이 충분하지 않음
③ 학습 반복이 많음(딥러닝의 경우)
④ 데이터 불균형(정상환자 - 암환자의 비율이 95: 5)
▶ 과적합 해결 - 테스트 데이터의 분리
(예시) 시험을 잘 보는 방법: 책으로 공부할 뿐 아니라 모의고사를 열심히 풀어보는 것
- 테스트 데이터의 분리
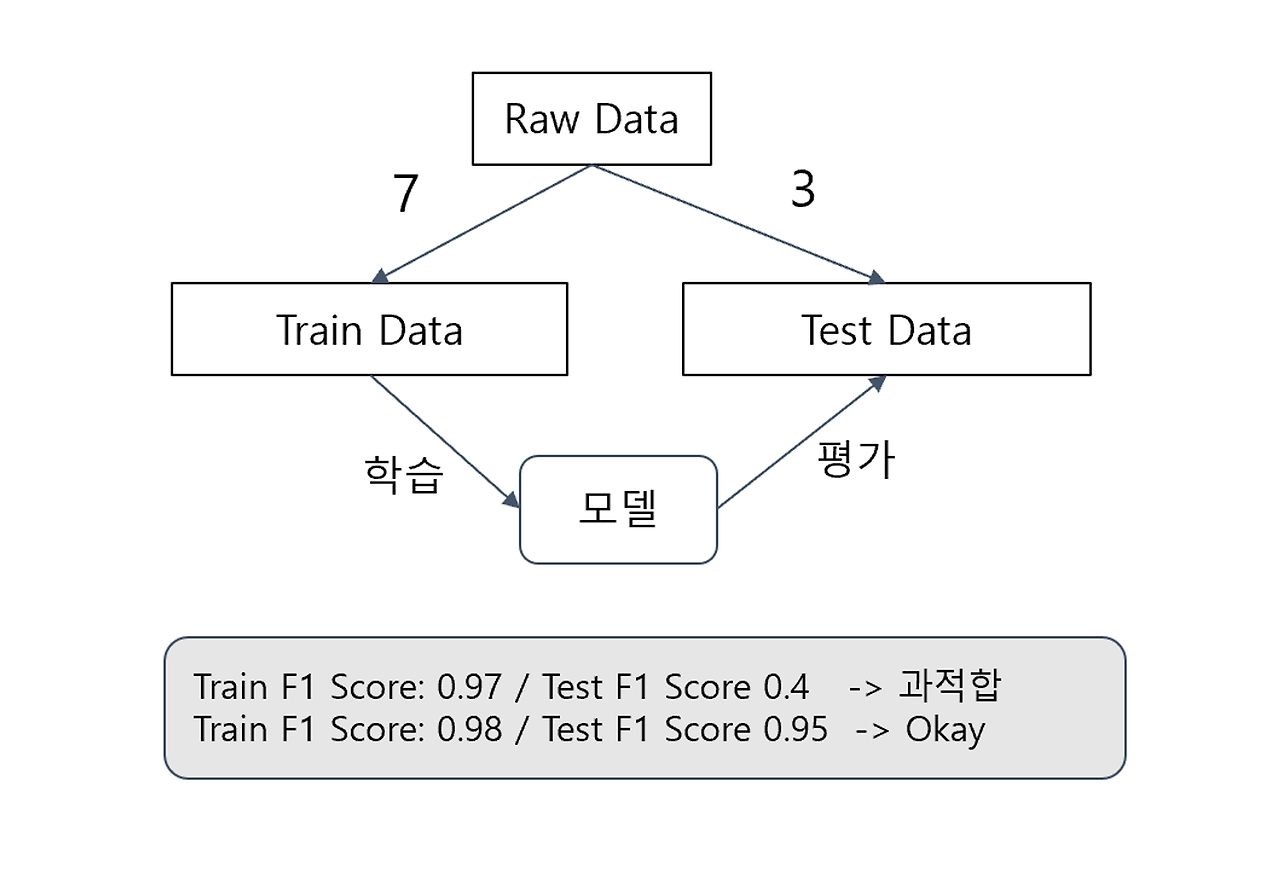
└ 학습 데이터(Train Data): 모델을 학습(fit)하기 위한 데이터
└ 테스트 데이터(Test Data): 모델을 평가 하기 위한 데이터
└ 학습 및 테스트 데이터의 F1-Score 값이 차이가 크지 않아야 함 (크면 과적합)
- 함수: sklearn.model_selection.train_test_split
* 머신러닝 모델을 만든다면 무척 많이 쓰게 될 함수
└ 파라미터
· test_size: 테스트 데이터 세트 크기 (ex. 70%)
· train_size: 학습 데이터 세트 크기 (ex. 30%)
· shuffle: 데이터 분리 시 섞기(random)
· random_state: 호출할 때마다 동일한 학습/테스트 데이터를 생성하기 위한 난수 값.
* 평가 학습 코드를 실행할 때마다 값이 바뀌면 동일한 결과값을 얻기 어렵기 때문에 숫자 고정 필요
· stratify: 본 데이터의 수치 및 범주간 비율을 보존 하면서 분리하는 것 (영어로 층을 이루다는 뜻)
└ 반환 값(순서 중요)
· X_train, X_test, y_train, y_test
· X_train, X_test는 학습/테스트 데이터의 x 변수(여러개), y_train, y_test는 학습/테스트 데이터의 y변수(1개)
- 데이터 분리 시 유의할 점
: 원본 데이터를 스케일링을 하고, 스케일링을 마친 데이터를 학습/평가 데이터로 나누면 안됨.
: 스케일링할 경우 학습데이터에서 가져와서 테스트 데이터에 적용해야 함
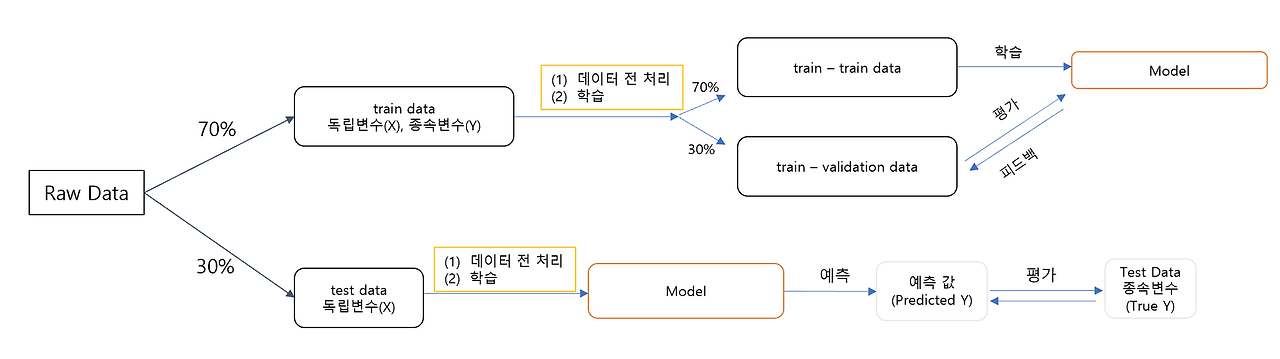
5) 데이터 전체 프로세스 정리
① 데이터 로드 & 분리
- train / test 데이터 분리
② 탐색적 데이터 분석(EDA)
- 분포확인 & 이상치 확인
└ 이상치는 ESD(mean + 3*std), IQR(Q3 - Q1, Qn + 1.5*IQR) 값으로 확인
③ 데이터 전처리
- 결측치 처리: fillna(), dropna()
└ 수치형(평균값 대치) : Age
└ 범주형(최빈값 대치): Embarked
└ 삭제 : Cabin, Name
- 전처리
└ 수치형: Age, Fare, Sibsp+Parch / 표준화(standardscaler), 정규화(minmaxscaler)
└ 범주형
· 레이블 인코딩(LabelEncoder): Pclass, Sex
· 원- 핫 인코딩(OneHotEncoder): Embarked
④ 모델 수립
⑤ 평가
(실습) 코드는 별첨 / keggle 제출 완료!
6) 교차 검증과 GridSearch
▶ 교차 검증(Cross Validation)
: 데이터 셋을 여러 개의 하위 집합으로 나누어 돌아가면서 검증 데이터로 사용하는 방법
: 테스트 데이터 분리 방법의 경우, 과적합 해결을 위한 것이긴 하나 고정된 테스트 데이터가 존재해 과적에 취약
- K-Fold Validation
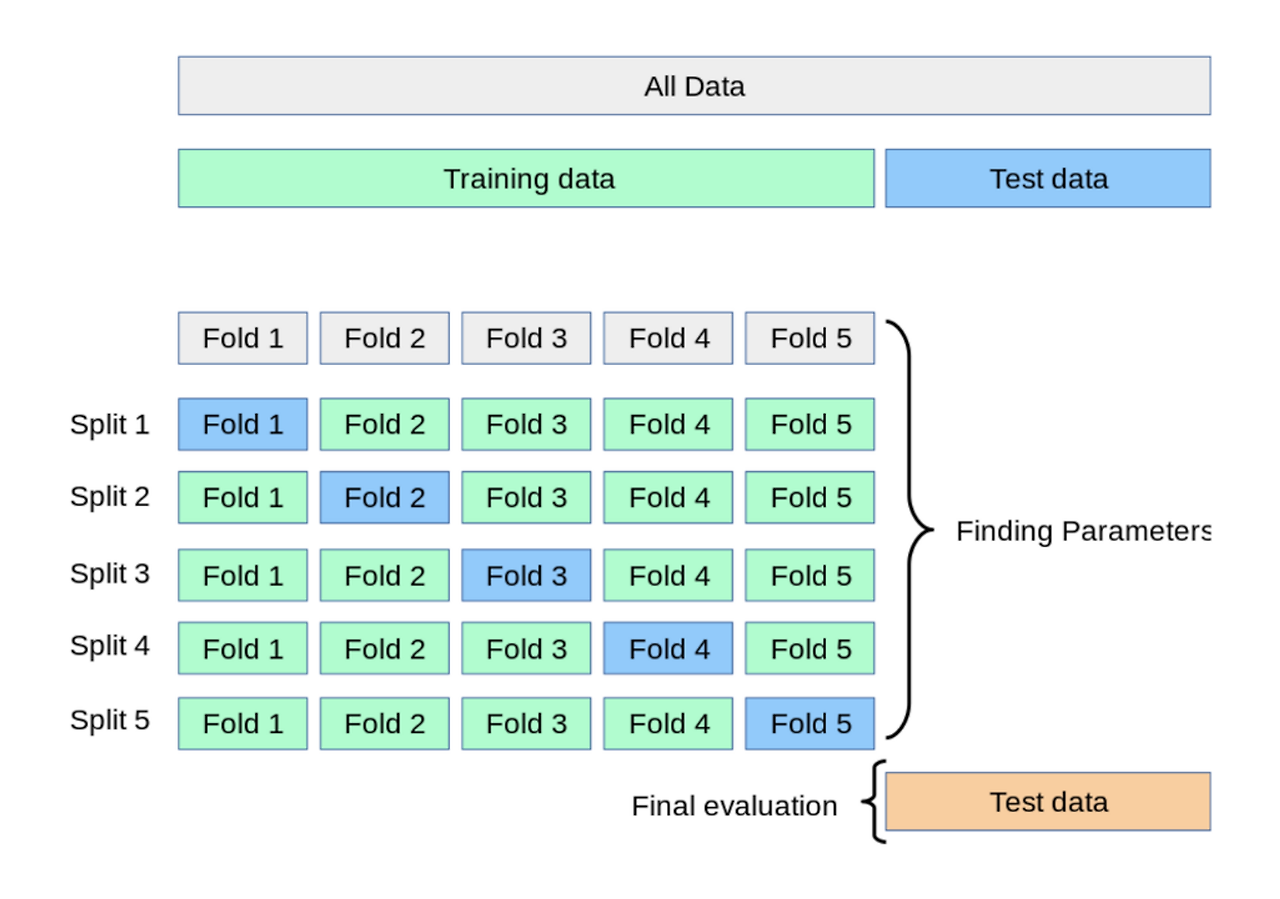
└ 정의: Train Data를 K개의 하위 집합으로 나누어 모델을 학습시키고 모델을 최적화 하는 방법(K=분할 수)
· Split 1: 학습용(Fold 2~5), 검증용(Fold1)
· Split 2: 학습용(Fold1, 3~5), 검증용(Fold2)
· Split 5까지 반복 후 최종 평가
└ 특징: 데이터가 부족할 경우 유용합니다.(반복 학습)
└ 함수
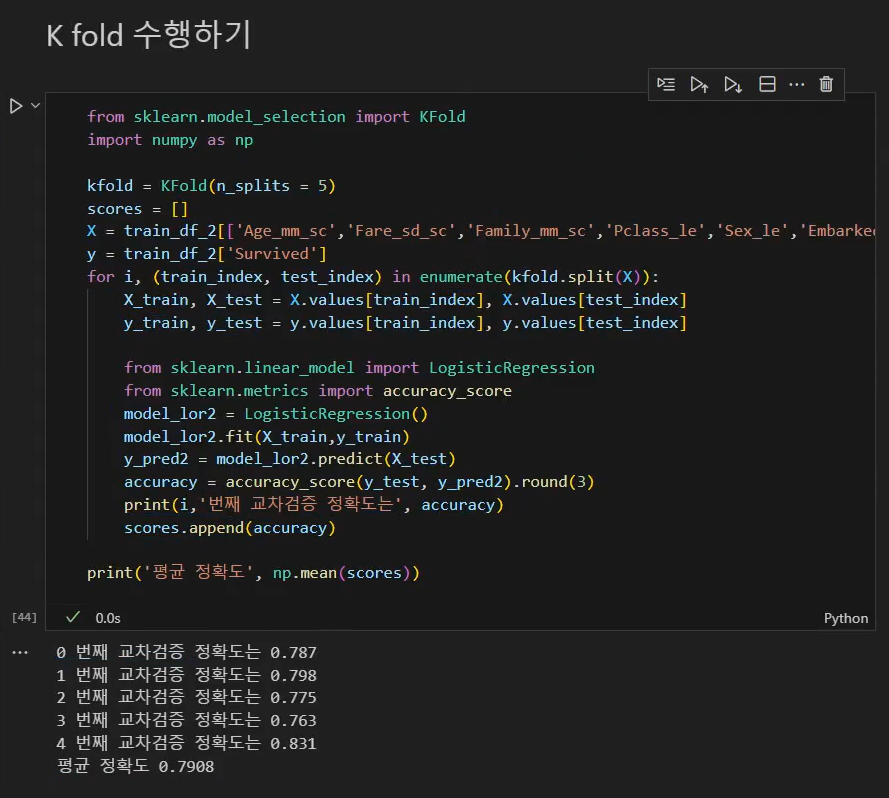
· skelarn.model_selection.KFold
· sklearn.model_selection.StrifiedKFold: 불균형한 레이블(Y)를 가지고 있을 때 사용
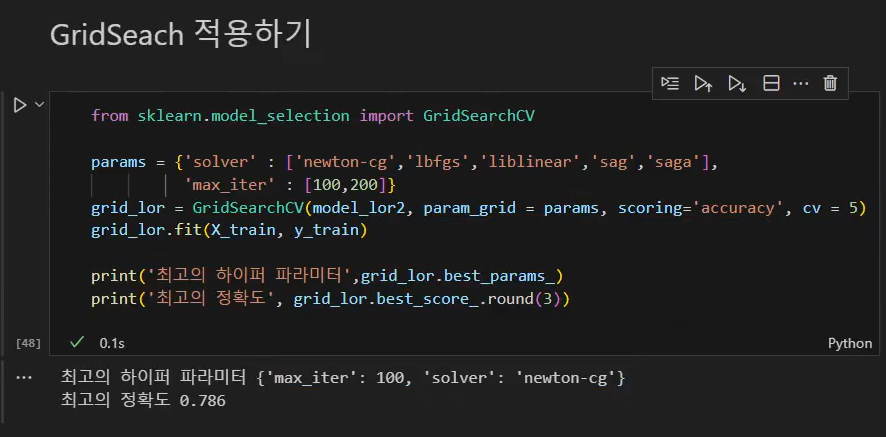
▶ 하이퍼 파라미터 자동적용하기 - GridSearchV
- 하이퍼 파라미터(Hyper Parameter): 모델을 구성하는 입력 값 중 사람이 임의적으로 바꿀 수 있는 입력 값
- Grid Search: 다양한 값을 넣고 실험할 수 있도록 하이퍼 파라미터 값을 자동화해주는 것
7) 데이터 분석 프로세스 정리
'TIL' 카테고리의 다른 글
| [240205] SQL: 코드카타 119~121 & 파이썬: 코드카타 29~30 (0) | 2024.02.05 |
|---|---|
| [240201-02] 머신러닝 - 회귀/분류 모델링 심화, 비지도 학습, 딥러닝 (0) | 2024.02.02 |
| [240131] SQL: 코드카타 118 & 파이썬: 코드카타 28 (0) | 2024.01.31 |
| [240130-31] 머신러닝 - 선형회귀, 로지스틱회귀 (1) | 2024.01.31 |
| [240130] SQL: 코드카타 117 & 파이썬: 코드카타 27 (0) | 2024.01.30 |

